Özel Görelilik Kuramı Konu Anlatımı

 Özel Görelilik Kuramı Konu Anlatımı

Newton Mekaniği 200 yıldan fazla bir süre fiziksel bilimlerin harika bir aracı oldu. Ona dayalı bir bilim ve teknoloji çağı yaratıldı. Halen bu çağın harikulade nimetlerinden yararlanıyoruz. Ama fizikçiler daha 19.yüzyıla girilirken, Newton Mekaniği‟nin bazı doğa olaylarını açıklamakta yetersiz kaldığını sezmeye başlamışlardı. Nitekim, 1884 yılında Lord Kelvin Baltimore konferanslarında “Fizik üzerinde dolaşan 19.yy bulutarı” „ndan sözederek , söz konusu olaylardan bazılarını sıralıyordu. Newton Mekaniği‟nin açıklayamadığı doğa olaylarından bazılarını sıralayabiliriz:

1. Işığın bir dalga hareketiyle yayıldığı genel kabul görmüştü, ama o dalgayı taşıdığı varsayılan ve uzayı dolduran ortamın (eter) var olduğunun kabul edilmesi çelişki yaratıyordu (Michelson-Morley deneyi).
2. Elektrik ve Magnetizma denklemleri Newton Mekaniğinin temeli olan mutlak uzay ve mutlak zaman kavramlarıyla çelişiyordu.

3. Newton hareket yasalarıyla Merkür gezegeninin yörüngesi çok büyük bir duyarlılıkla hesaplanabiliyordu. Ancak, gözlem sonuçlarıyla hesap sonuçları arasında beliren küçük ama rahatsız edici bir fark ortaya çıkıyor, ama nedeni açıklanamıyordu.
4. Çok düşük ısıdaki maddeler Newton yasalarına göre hareket
5. Newton fiziğine göre, sabit ısıdaki bir ocağın sonsuz enerjisi olmalıydı.

 

Bu ve benzeri sorunların giderilebilmesi için fizikçiler çok uğraştılar, ama sonuç alamadılar. Sonuç çıkmamasını bugün doğal karşılıyoruz, çünkü mutlak uzay ve mutlak zaman kavramlarına dayalı çözüm getirilemezdi. Başka bir deyişle, ortaya çıkan sorunların Newton Mekaniği ile çözülebilmesi olanaksızdı.

Çözüm yönünde ilk doğru adımı Lorentz attı. İkinci önemli adım ise, zamanın ünlü matematikçisi Poincare‟den geldi. Bu ikisi, birbirlerinden bağımsız olarak, Görelilik Kuramı için gerekli bütün matematiksel araçları ortaya koymuşlardı. Ama onlar ortaya koydukları matematiksel formüllere fiziksel anlam veremediler. Onları yorumlayıp, evrene bakışımızı değiştiren teoriyi ortaya atan Albert Einstein oldu. 1905 yılında Özel Görelilik kuramını ve 1915 yılında da Genel Görelilik kuramını ortaya koydu. Bu iş, 1800 yıllık Aristo evren modelini 1543 yılında Copernicus‟un yıkışından çok daha görkemli oldu.

Özel Görelilik Kuramını Ortaya Çıkaran Kuramsal Nedenler

Özel Görelilik kuramının iki temel dayanağı vardır:

1. Işık hızı sabittir. Gözlemcilerin birbirlerine göre hızları ne olursa olsun, ışık hızı bütün gözlemciler için aynıdır.

 

2. Fizik yasaları bütün eylemsiz konaç sistemlerinde aynıdır. Bunun anlamı şudur, bir referans noktasına göre sabit duran bir gözlemci ile o referans noktasına göre düzgün doğrusal hareket eden başka bir gözlemci, bütün hareket yasalarını aynı algılarlar.

Bu dayanaklardan yola çıkan Einstein, Newton Mekaniğinin temeli olan mutlak uzay ve mutlak zamanın var olmadığını, zamanın ve uzunluğun gözlemcinin kullandığı konaç sistemine bağlı olarak değiştiğini göstermiş, momentum ve enerji tanımlarına farklı bir bakış getirmiştir. Şimdi bunları açıklamaya çalışalım.

Konuşlanma Sistemleri (Frames of Reference)

Bir cismin hareketini belirleyebilmek için onun ne zaman, nerede olduğunu bilebilmemiz gerekir. Nerede olduğunu söyleyebilmek için bir koordinat sistemine gerekseme vardır. Koordinat sisteminde nerede hangi zamanda bulunduğunu söyleyebilmek için de bir saat‘e gereksememiz vardır. Burada saat sözcüğü, zamanı ölçen bir boyut gibi düşünülebilir. Şimdilik böyle düşünmekte bir sakınca yoktur, ama görelilik kuramında, zaman (saat) kavramı kartezyen koordinat sistemindeki eksenlerinden farklı bir işleve sahip olacaktır.

 

Cismin uzayda (doğru, düzlem ya da 3-boyutlu olabilir) yerini belirtecek bir koordinat sistemine ek olarak zamanı belirtecek bir boyut (saat) eklediğimizde bir konuşlanma sistemi (frame of reference) elde ederiz.

Eylemsiz Konuşlanma Sistemleri (Inertial Frames) Newton ‘un eylemsizlik yasası‟nı anımsayalım:

1. Bir cisim hareketsiz ise ve hiç bir kuvvet ona etki etmiyorsa, o cisim hareketsiz kalmaya devam eder;
2. Bir cisim düzgün doğrusal bir hareket (bir doğru boyunca sabit bir hızla hareket) yapıyorsa ve hiç bir kuvvet ona etki etmiyorsa, o cisim düzgün doğrusal hareketine devam eder;

 

Fizik derslerinde öğrendiklerimizin aksine, iki yüz yıl boyunca bilimin ve teknolojinin temeli olan bu yasa doğru değildir; en azından, her yerde doğru değildir. Bu yasanın doğruluğu, hangi konuşlanma sistemine göre konuştuğumuza bağlıdır. Buna örnekler verebiliriz:

 

• Koordinat sisteminin merkezi ile cismin kütle merkezi çakışık iseler, cisim nasıl hareket ederse etsin, sözkonusu koordinat sistemine göre hareketsizdir.
• Yerküre çevresinde hızla dönen bir uzay gemisindeki kumanda masası, gemiye göre, hareketsizdir; ama o gravitasyonun ve gemiyi yörüngede döndüren kuvvetin etkisi altındadır.
• Bir arabanın boş bagajına konulmuş bir top düşünelim. Araba hızlanırken, top bagajda geriye doğru, araba fren yaparak yavaşlarken ileriye doğru yuvarlanır. Oysa bagajdaki topa etki eden bir kuvvet yoktur.

 

O halde, ne zaman Newton’un eylemsizlik yasasından sözediyorsak, o yasanın geçerli olduğu bir konuşlanma sistemine göre konuşuyoruz demektir. Bu tür konuşlanma sistemlerine Eylemsiz Konuşlanma Sistemleri diyeceğiz. Başka bir deyişle, bir Eylemsiz Konuşlanma Sistemi ivmesiz bir koordinat sistemidir. Dolayısıyla, bir eylemsiz koordinat sistemi , bir yere göre, sabittir ya da düzgün doğrusal hareket eder.

 

Böyle sistemlerin var olup olmadıkları düşünülebilir. Şimdilik, şunu söylemekle yetineceğiz. Bir eylemsiz konuşlanma sistemi varsa, sonsuz tane eylemsiz konuşlanma sistemi kurulabilir. Gerçekten, birinci sisteme göre düzgün doğrusal hareket eden her konuşlanma sistemi eylemsiz bir sistemdir.

İçinde eylemsizlik yasasının geçerli olmadığı konuşlanma sistemlerine eylemli konuşlanma sistemleri denilir.

Bu sistemler, eylemsiz sistemlere göre bir ivmeye sahip sistemlerdir.

Eylemsiz Sistemlerde Fizik Yasaları

Eylemsiz sistemlerde fizik yasaları aynıdır. Daha açık söylemek gerekirse, birisi ötekine göre düzgün doğrusal hareket eden iki eylemsiz sistemin birisinde geçerli olan fizik kuralları diğerinde de aynen geçerlidir. Dolayısıyla, bir eylemsiz sistemin ötekine üstünlüğü yoktur. Bu özelik, fizik yasaları için istediğimiz eylemsiz konuşlanma sistemini seçebileceğimiz anlamına gelir.

Galilei dönüşümü

K ve K’ iki eylemsiz konuşlanma sistemi olsun ve K’ sistemi K ya göre sabit v hızıyla Ox doğrultusunda hareket etsin. Bir P noktasının (cisminin – şekildeki top) bu iki sisteme göre konaçları (koordinatları), sırasıyla, (x,t) ve (x’,t’) olsun. Bu konaçlar arasında

x’ = x – vt , t’ = t

bağıntısı vardır. Burada, her iki sistemde zaman koordinatlarının (saatlerin) aynı olduğunu varsayıyoruz (t = t’). K sistemi içindeki bir gözlemciye göre bir t anında topun yatay eksendeki konumu x = x’ + vt dir. K’ sistemi içindeki bir gözlemciye göre ise aynı t = t’ anında topun yatay eksendeki konumu x’ dür. Yukarıdaki bağıntıdan

x = x’ + vt ,  t = t’

Yazabiliriz. Galilei dönüşümü denilen bu bağıntıları kullanarak, cismin bir eylemsiz sistemdeki konumunu biliyorsak, öteki sistemdeki konumunu daima bulabiliriz.

Yukarıda söylediğimiz kuralı, şöyle de ifade edebiliriz:

 

“Fizik kuralları Galilei dönüşümü altında değişmezler.”

Newton’un İkinci Yasası

Bir F kuvveti kütlesi m olan bir cisme etki ederse cismin kazanacağı ivme F kuvvetiyle doğru, m kütlesiyle ters orantılıdır. Bu demektir ki

1. Ağır cisimleri ivmelendirmek için daha büyük kuvvet gerekir, ve
2. Etki eden kuvvet büyüdükçe, cismin ivmesi

Newton’un İkinci Yasası eylemsiz konuşlanma sistemlerinde geçerlidir. a ivme olmak üzere, sözkonusu yasayı şu formülle ifade ederiz:

F = ma

 

Bu yasa, eylemsiz bir K sisteminde geçerli ise, başka eylemsiz bir K’ sisteminde de geçerlidir. Böyle olduğunu göstermek kolaydır. Gerçekten, K ve K’ sistemlerindeki hızları, sırasıyla u, u’ ile ivmeleri a, a’ ile gösterirsek,

x’ = x – vt    ,         t’ = t

bağıntısından, yolun zamana göre türevini alarak, hızlar arasında

u’ = u – v

bağıntısını buluruz. Benzer şekilde, hızın zamana göre türevini alarak, ivmeler arasında

a’ = a

bağıntısını hemen çıkarabiliriz.

 

Eylemli (ivmeli) Sistemlerde Fizik Kuralları

Eylemli sistemlerde Newton’un ikinci hareket yasası geçersizdir. 

Uzayda yerküre etrafında dönen bir uzay gemisini düşünelim. Gravitasyon gemiye ve gemi içindeki her şeye etki eder, ama gemi içindeki hiç bir cisim gemiye göre ivme kazanamaz. Bu duruma ağırlıksız ortam denir. Ağırlıksız ortam gravitasyonsuz ortam demek değildir. İşin aslına bakarsak, gravitasyonsuz olsa, uzay gemisi dünya etrafındaki yörüngesinde duramaz, uzaklaşırdı. Gerçekte olan şey şudur: Uzay gemisi ve içindeki her şey dünya merkezine doğru devamlı düşme halindedirler.

Fizik derslerinden anımsayacağınız gibi, (hayali) bir merkezkaç kuvvet uygulayarak eylemli sistemlerde de F = ma yasasını geçerli kılabiliriz. Merkezkaç gibi hayali kuvvetlere eylemsizlik kuvvetleri diyoruz. Eylemsizlik kuvvetleri, cisme ivme kazandırmaya çalışan kuvvet(lere) karşı duran kuvvetlerdir.

Şimdilik, eylemsiz ve eylemli sistemlerde fizik yasalarının farklı uygulanacağını bilmemiz yetecektir.

Özel ve Genel Görelilik Kuramları 

Görelilik Kuramı, hızı ışık hızına yaklaşan cisimlerin hareketini inceler. Işığın hızı c=3×10⁸m/sn (yaklaşık 300 000 km/sn) dir. Newton‘un ikinci yasası, hızı ışık hızına yaklaşan cisimler için geçerliğini yitirir. Görelilik Kuramı, Newton Mekaniğinin bu eksikliğini giderir.

Özel Görelilik Kuramı, yalnızca eylemsiz konuşlanma sistemlerine uygulanır. Genel Görelilik Kuramı, eylemli sistemlere de uygulanır. Bu konuşmada önce özel görelilik kuramını ele alacağız. Özel Görelilik Kuramını 1905 yılında ortaya atan Albert Einstein, genel görelilik kuramı için tam 10 yıl harcamış ve kuramını 1915 yılında yayınlamıştır.

Özel Görelilik Kuramı oldukça basit matematiksel formüllerle açıklanabilir. Genel Görelilik Kuramını açıklamak için farklı matematiksel yapılar kullanılabilir. Einsten, Riemann geometrisine ve tensör hesaba dayalı bir yöntem izlemiştir. Aradan gen yüzyıl boyunca, genel görelilik kuramını açıklamak için çok daha elverişli cebir ve geometri yapıları ortaya konulmuştur. İki kuram arasındaki farkı ortaya koymak için, aşağıdaki tabloya bakalım:

 

Maddenin hızı		Eylemsiz Sistemlerde		Eylemli Sistemlerde
Işık hızından çok çok az		Newton yasaları		Newtonyasaları + Hayali Kuvvetler
Işık hızına yakın		Özel Görelilik Kuramı		Genel Görelilik Kuramı

 

Biraz Tarih

Newton hareket yasaları 17.yüzyılda ortaya kondu. Newton Mekaniği diye adlandırılan bilim dalına esas olan Newton hareket yasaları, bilimde atılmış en büyük adımlardan biridir. 18. ve

19. yüzyıllarda Newton Mekaniği sayesinde muazzam bir teknoloji yaratıldı, gök cisimlerinin hareketleri belirlendi. Bu gün bile Newton Mekaniği yok sayılırsa, elimizde 20. yüzyıl teknolojisi yok olur.

Maxwell

Newton hareket yasaları çok önemli olmakla beraber, ışık hızına yakın hızlarda hareket eden cisimlere uygulanamıyor. 19. yüzyılın ortalarında Maxwell elektrik ve magnetizma arasındaki ilişkileri kuran önemli bir kuram geliştirdi. Bu kurama göre, elektromagnetik dalgalar ışık hızıyla yayılmaktadır. Başka bir deyişle, ışık, elektromanyetik dalgalar halinde yayılmaktadır.

Newton hareket yasalarını belirleyen matematiksel denklemler Galilei dönüşümü altında değişmiyordu (invariant). Ama, Maxwell denklemlerinin Galilei dönüşümü altında değiştiği (non-invariant) görüldü. Maxwell denklemi bir eylemsiz sistemde geçerli kabul edilse, ışık hızını belirleyen denklemler başka bir eylemsizlik sistemine dönüştüğünde tamamen değişmektedirler.

Bu demektir ki, Newton Mekaniğinde kabul edildiği gibi, fizik yasaları her eylemsiz sistemde aynı değildir.

Bu gerçeğin ortaya çıkması, 20. yüzyıl başlarında fizik yasalarına bakışımızı tümüyle değiştiren bir olgu oldu.

Bu güçlüğün çözümü için çeşitli görüşler ileri sürüldü. En geçerli görünen görüş “ether” kuramıydı. Ses dalgalarının yayılabilmesi için hava, su vb bir ortamın olması nasıl gerekiyorsa, ışık dalgalarının da boşlukta yayılabilmesi için bir ortama gereksinimi vardır. Bütün uzay boşluğunu doldurduğu varsayılan bu maddeye ether denildi.

Maxwell denkleminin belirlediği ışık hızı ether’e göreli olarak belirleniyor olmalıydı. Eğer gözlemcinin gözlediği ışık hızı Maxwell denkleminin belirlediğinden farklı ise (ki bu çok

küçük bir farktır), bunun nedeni, fizik kurallarının her eylemsiz sistemde aynı olmaması değil, gözlemcinin eylemsizlik konuşlanmasının ether’e göre hareket ediyor olmasıydı.

Michelson-Morley

Yüz yıl kadar önce Michelson & Morley adlı iki bilim adamı, uzay boşluğunun ether ile dolu olduğu varsayımını çürüttüler. Aslında, deneylere başlarken ether’in varlığına inanıyor ve onu kanıtlamak amacını güdüyorlardı.

Beklentilerin aksine, boşlukta ether olmadığı, ışık hızının gözlemcinin hızına (onun bulunduğu eylemsiz sistemin hızına) bağlı olmadığı, her sistemden aynı hızla göründüğü kanıtlandı.

Ortaya oldukça ilginç bir durum çıkmıştı. Maxwell denklemlerine göre ışık hızı bir eylemsiz sistemden ötekine değişiyordu. Ama Michelson & Morley deneyi, ışığın her eylemsiz sistemden aynı göründüğü sonucunu veriyordu.

Şimdi problem şuna dönmüştü: Işığın hızı neden her eylemsiz sistemden aynı görünüyordu? Bunun yanıtı ancak, eşzamanlılık kavramımızın değişmesiyle verilebilirdi. Bunu 1905 yılında Einstein, Özel Görelilik Kuramı’nı ortaya atarak çözdü.

Özel Görelilik Kuramı özetle şunu söylüyor. Işığın hızının her eylemsiz sistemden aynı (sabit hız) görünmesinin nedenini anlamak için, bir sistemden ötekine geçerken kullandığımız dönüşümleri değiştirmeliyiz. Galilei dönüşümleri dediğimiz

dönüşümler ışık hızı için yetersizdir. Onun yerine Lorentz Dönüşümleri denilen

dönüşümler kullanılmalıdır:

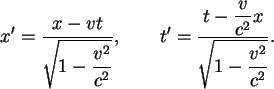
Buradan görüldüğü gibi, bir frame ötekine göreli olarak sabit v hızıyla gidiyorsa ve v<<c ise, Lorentz dönüşümü Galilei dönüşümüne indirgenmiş olur. O halde, Galilei dönüşümü, Lorentz dönüşümünün özel bir halidir. Gerçekten, Maxwell’e kadar Galilei dönüşümüyle bir sorun yaşanmamış olmasının nedeni, ele alınan v hızlarının ışık hızından çok çok küçük olmasıdır.

Bu söylediklerimizin sağlandığını matematiksel olarak kolayca gösterebiliriz. Gerçekten, Işık hızı‘nın (x,t) and (x’,t’) konuşlanma sistemlerinde (frame) içinde aynı olduğunu görmek için aşağıdaki usavurma yeterlidir. t’=t=0 anında x’=x=0 başlangıç noktasından bir ışık hüzmesi yola çıksın. Işığın hızı c olduğundan, t=T anında, sözkonusu ışık hüzmesi (x,t) sistemi içinde x=cT noktasına ulaşacaktır. Oysa, öteki sistem içinde ışığın konumu olarak gözlenecektir.

O halde, (x’,t’) sistemi içinde ışğın hızı

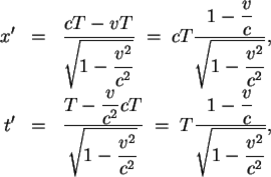
olacaktır.

Eş Zamanlılık

Lorentz Dönüşümü‘nden sezinlenebileceği gibi, t=t’ gibi basit bir bağıntı olmayacağına göre zaman göreli bir kavram halini almaktadır. Gerçekte bunun anlamı eşzamanlılık kavramının hangi eylemsiz konuşlanma sistemi içinde olduğumuza bağlı olduğudur. Bu durum, ışık hızının hangi eylemsiz konuşlanma sistemi içinde olduğumuza bağlı olmadığından çıkar.

Hareket halindeki bir tren vagonunun tam ortasında bir lamba olsun. Lamba yandığında ışık hüzmesi hem trenin gidiş yönüne hem onun ters yönüne c=3×10⁸m/sec hızıyla yayılacaktır.

Vagonun içindeki bir gözlemci, ışığın vagonun önüne ve arkasına aynı anda (eş zamanlı) ulaştığını görecektir.

Öte yandan, tren dışındaki bir gözlemci için durum farklıdır. Işığın hızı, gözlemcinin içinde bulunduğu eylemsiz sisteme bağlı olmaksızın, her gözlemciye göre aynıdır ve vagonun her iki yönüne doğru c hızıyla gider. Vagonun arkası kendisine doğru gelen ışığa yaklaşırken, vagonun önü kendisine doğru gelen ışıktan uzaklaşmaktadır. Dolayısıyla, ışık vagonun arkasına daha çabuk, vagonun önüne daha geç ulaşacaktır. Demek ki, bu iki olay, yerdeki gözlemci için eş zamanlı değildir.

Görüldüğü gibi, tren içindeki gözlemciye eşzamanlı görünen iki olay tren dışındaki gözlemciye farklı zamanlarda olan iki olay olarak görünmektedir.

Oyunu biraz daha eğlenceli kılmak için, trenden daha hızlı giden bir yarış arabası içindeki gözlemcinin olayları nasıl göreceğine bakalım.

Gene, ışığın hızının, gözlemcinin içinde bulunduğu eylemsiz sisteme bağlı olmaksızın, her gözlemciye göre aynı olduğunu ve vagonun her iki yönüne doğru c hızıyla gittiğini anımsayalım. Yarış arabası trenden daha hızlı olduğu için, arabadaki gözlemciye göre tren ters yönde gitmektedir. Dolayısıyla, vagonun önü kendisine doğru gelen ışığa yaklaşırken, vagonun arkası kendisine doğru gelen ışıktan uzaklaşmaktadır. Dolayısıyla, ışık vagonun arkasına daha geç, vagonun önüne daha erken ulaşacaktır. Demek ki, bu iki olay, arabadaki gözlemci için eşzamanlı değildir.

Sonuç: Bir vagonda geçen iki olayın kronolojik sırası yerdeki, vagondaki ve trenden hızlı giden bir araçtaki üç gözlemci tarafından farklı görünmektedir. O halde, farklı eylemsiz sistemlerde eşzamanlılık olamaz.

Işıktan Daha Hızlı Hareket

Eğer öncelik, eşzamanlılık ve sonralık kavramları gözlemciye göre değişiyorsa, bir olayın başka bir olayı yarattığı nedensellik kavramını nasıl açıklayacağımızı ciddi olarak düşünmeliyiz.

Bunu biraz açıklamakta yarar vardır. Eğer bir A olayı başka bir B olayının olmasının nedeni ise, A olayı B olayından önce olmalıdır. Ama, bir gözlemci A olayının B olayından önce olduğunu, başka bir gözlemci ise A olayının B olayından sonra olduğunu gözlüyorsa, nedensellik konusunda bir uyuşmazlık ortaya çıkacaktır.

Bir A noktasından atılan bir ok B noktasındaki elmayı vursun. Okun atılışına A olayı, elmanın vuruluşuna da B olayı diyelim.

Önceki bölümde ele aldığımız uzay-zaman diyagramlarını bu iki olay için tekrarlayalım:

1. A da ok atıldı
2. Atılan ok A ve B yi birleştiren doğru boyunca yol aldı.
3. Ok B ye ulaşınca elmayı

 

(x,t) sisteminde, ok atıldıktan sonra elma vurulur. (x’,t’) sisteminde, okun atılışı ile elmanın vuruluşu eşzamanlıdır . (x”,t”) sisteminde, elma ok atılmadan önce vurulmuş olacaktır. Bu çelişki nereden geliyor? Biraz düşününce, çelişkinin kaynağını göreceğiz. A dan B ye giden okun ışık hızından daha hızlı hareket ettiğini varsayıyoruz. Oysa, görelilik kuramına göre hiç bir cisim ışık hızından daha hızlı gidemez.

Saatlerin Eşzamanlaştırılması (Synchronization)

Eşzamanlılık kavramının göreli oluşu bazı sonuçlar doğuracaktır. Bu sonuçlardan birisi şudur: Bir frame içinde senkronize edilen saatler başka bir frame içinden senkronize edilmemiş görünür.

Zaman Genişlemesi (Time Dilation)

Eşzamanlılık kavramının göreliliğinin önemli sonuçlarından birisi şudur: Farklı eylemsiz konuşlanma sistemlerinde zamanın akış hızı farklıdır. Buna zaman genişlemesi (time dilation) diyoruz.

İki saatin hızını karşılaştırmak için, şöyle basit bir yol izlenebilir.

1. Bir başlangıç anı seçilir ve her iki saatin o anda (aynı anda) aynı zamanı göstermesi (senkronize) sağlanır.
2. Aradan belli bir süre geçtikten sonraki bir anda (aynı anda) her iki saat

Bu işi yaparken, parantez içindeki “aynı anda” deyimini söylemeye bile gerek görmüyoruz. Çünkü o yapacağımız mukayese için doğal olarak gereklidir. Oysa “aynı anda” deyimi “eşzamanlılık” deyimidir. Ama biliyoruz ki, farklı gözlemcilere göre “eşzamanlılık” olamaz.

Bunu uzay-zaman çizeneğinden görebiliriz. (x,t) ve (x’,t’) eylemsiz sistemlerinin başlangıç noktaları belli bir anda çakışık olsun. Ayrıca, bu çakışma anında saatleri senkronize edilmiş olsun (Yukarıdaki 1. Adım). (x,t) sistemine göre (x’,t’) sistemi sabit bir v hızıyla hareket ediyor olsun. Bir süre sonra, saatler birbirinden uzaklaşacak ve onları üst üste çakıştırıp aynı anda gösterdikleri zamanı okuma olanağı kalmayacaktır. (x,t) sistemindeki gözlemci belli bir anda kendi saati ile (x’,t’) sistemindeki saati mukayese edince, öteki saatin geri kaldığını görecektir. Tersine olarak, (x’,t’) sistemindeki gözlemci aynı anda kendi saatini (x,t) sistemindeki saat ile mukayese edince, öteki saatin geri kaldığını görecektir. Başka bir deyişle, her gözlemci, ötekinin saatinin yavaş gittiğini görecektir. Bunun nedeni, eşzamanlılık olduğunu varsaymamızdır.

Lorentz Daralması

Eşzamansızlık kavramının sonuçlarından birisi de uzunlukların gözlemciye bağımlı olarak değişmesidir.

Bir şeyin uzunluğunu nasıl ölçeriz? Uzunluğu ölçülecek cismi bir eksen (skalası olan bir doğru) üzerindeymiş gibi düşünür ve cismin iki ucunun skaladaki karşılıklarını okur, bunlar arasındaki farkı buluruz. Bulduğumuz fark o cismin uzunluğudur.

Acaba,  konu  bu  kadar  basit  midir? Basit  olmadığını  bir  örnekle  açıklayalım.

Bir tren vagonunun uzunluğunu ölçmek isteyelim. Tren istasyonda duruyor iken, vagonun iki ucu arasındaki rayın uzunluğunu ölçersek, trenin uzunluğunu bulabiliriz. Ama tren hareket ediyorsa ne yapabiliriz? Vagonun arka ucunun ray üzerindeki izdüşümünü işaretleyip, ön ucu için aynı işi yapmak üzere öne doğru çok çok hızla gitsek bile, tren hareket halinde olduğu için belli bir yol alacak ve ölçümlememiz vagunu daha uzun gösterecektir. Tersine olarak, önce vagonun önünden ölçümlemeye başlasak, bu kez tren olduğundan daha kısa çıkacaktır. Tabii, pratikten kaynaklanan bu sorunu çözmek kolay görünüyor. Vagonun her iki ucun için ölçümlemeyi aynı anda (eşzamanlı) yaparız. Oysa bu iş, ancak aynı konaç sisteminde isek yapılabilir. Farklı konaç sistemlerindeki gözlemciler için eşzamanlılık yoktur.

Şimdi,  cismin  ya  da  eksenin  ötekine  göre  hareket  ettiğini  düşünelim.  Örneğin, Bu işi, ancak cisim ve eksen birbirlerine göre hareketsiz iseler yapabiliriz. Yani, her ikisi de aynı bir eylemsiz konuşlanma sisteminde iseler…

Vagon içindeki gözlemci, vagonun ön ve arkası arasındaki uzunluğu, kendi kon sistemine göre, vagonun ön ve arka duvarlarını eşzamanlı olarak eksen üzerine izdüşürerek, vagonun uzunluğunu L’ olarak ölçsün. Yerdeki gözlemci de kendi kon sistemine göre, vagonun uzunluğunu L olarak ölçsün. Trenin hızı v ise, Lorentz dönüşümüne göre L ile L’ arasında

bağıntısı vardır. Buradan görüldüğü gibi, L > L’ dür. Bu demektir ki, yerdeki gözlemci hareketli treni daha kısa görecektir. Bunun nedeni, farklı gözlemciler arasında eşzamanlılık olamayışıdır. Bu etkiye Lorentz Daralması (Lorentz contraction) diyoruz.

Hareketsiz iken cismin uzunluğuna onun doğal uzunluğu diyoruz. Bir cismin doğal uzunluğu, hareket halindeki uzunluğundan daha büyüktür. Başka bir deyişle, hareket eden cisimler (hareket yönünde) daha kısa görünürler. Lorentz Dönüşümü bu daralmanın oranını vermektedir.

Eylemsiz Kon Sistemlerinin Denkliği

Yerdeki bir gözlemciye göre (sabit eylemsiz kon sistemi), hareketli eylemsiz sistemdeki uzunlukların küçüldüğünü ve saatlerin yavaşladığını söyledik.

Öte yandan, trendeki bir gözlemciye göre, trenin eylemsizlik kon dizgesi sabittir, yerdeki eylemsiz kon sistemi ise (trene göre ters yönde) hareket etmektedir. Bütün eylemsiz kon sistemleri denk olduğuna göre, trenden bakınca yerdeki uzunlukların küçüldüğünü ve saatlerin yavaşladığını gözlemlemeliyiz.

İkizler Çatışkısı (The Twin Paradox)

Yirminci yaş gününde ikiz kardeşlerden birisi çok hızlı giden bir gemiyle uzay yolculuğuna çıksın. Seyahat, dünya zamanına göre yıllar (diyelim 40 yıl) sürsün. Dünyadaki konaç sistemine göre, hızlı uzay gemisinde zaman genişlemesi (yavaşlaması) olacağından, seyahat eden ikiz daha az yaşlanacaktır (diyelim 10 yıl). Geri döndüğünde, dünyadaki kardeşi 60 yaşında, kendisi ise 30 yaşında olacaktır.

Öte yandan, hareket göreli olduğu için, uzay gemisindeki konuşlanma sistemine göre, dünya gemiden hızla (ters yönde) uzaklaşmaktadır. Aynı nedenle, bu kez, gemideki ikiz 60 yaşında, dünyadaki ikiz ise 30 yaşında olacaktır.

Bu bir paradoks gibi görünmektedir.