İkizkenar ve Eşkenar Üçgen Konu Anlatımı: İkizkenar ve eşkenar üçgenlerin özelliklerini, geometrik formüllerini ve bu şekillerin pratik uygulamalarını öğrenin.
İkizkenar Üçgen
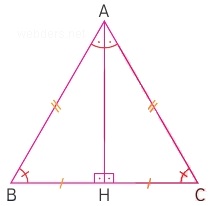
Kenarlarından ikisi birbirine eşit olan üçgene ikizkenar üçgen denir. Bir üçgende kenarların eşit olması o açılara bakan kenarların da eşit olması manasına gelir. Dolayısıyla ikizkenar üçgende hem açısal eşitlik hem de kenar uzunluğu açısından eşitlik vardır.
İkizkenar üçgende çizilen orta dikme hem yükseklik hem açıortay hem de kenarortaydır. Bu konuyla ilgili bilmemiz gereken en önemli özellik budur. Yukarıdaki şekilde |AH| doğru parçası bu üç işlevi de aynı anda görmektedir. Bu doğru parçası üçgeni eşit ve simetrik iki parçaya ayırır. Bir örnek üzerinden ikizkenar üçgenin bu özelliğini görelim.
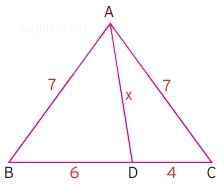
Yukarıdaki örnekte x uzunluğu sorulmaktadır. İki kenar uzunluğunun eşit olması bizi yükseklik ve kenar ortay elde etmeye teşvik etmektedir. Bu tarz sorular bu konuyla ilgili sorulan en kolay ve temel sorulardır. Bu sorunun çözümünü ise indirdiğimiz dikme ile şekil üzerinde gerçekleştirelim.
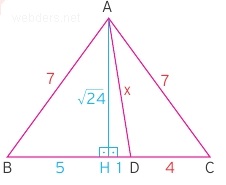
Dikmeyi indirdikten sonra aşağıdaki 10 birim uzunluktaki |BC| kenarı 5 birimlik iki parçaya ayrılır. Çünkü ikizkenar üçgende yüksekliğin aynı zamanda kenarortay olduğunu biliyoruz. Elde ettiğimiz yeni minik AHD üçgeninde ise x uzunluğunu Pisagor bağıntısı ile bulabiliriz. 1 + 24 = 25, √25 = 5 = x olur.
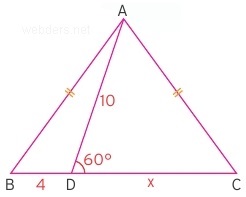
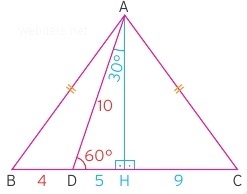
Dik üçgen özelliklerini de dahil ettiğimiz açılı bir örnek daha çözelim. Aşağıdaki üçgende 60 derecelik bir açı ikizkenar üçgenle birlikte verilmiş ve yine x uzunluğu sorulmaktadır.
Sorunun çözümü için yine dikme indiririz.
İndirilen dikme ile dikmenin indiği kenar ikiye eşit parçaya bölünmektedir ve 30- 60 – 90 üçgeni ortaya çıkmıştır. 90 derecenin karşısı 10 birim olduğu için 30 derecenin karşısı 5 birim olacaktır. Bu durumda dikme aynı zamanda kenarortay olduğu için ve de |BH| = 9 birim olduğundan |HC| de 9 birim olur. Bu durumda x = 9 + 5 = 13 birim olur.
İkizkenar Üçgenin Diğer Özellikleri
İkizkenar üçgenin yukarıda belirtilen özelliği en önemli özelliğidir ancak bunun dışında da problemleri kolaylaştıran birçok özellik vardır. Bu özelliklerin birçoğu birbiriyle bağlantılı olduğu için en önemli ve yaygın özellikleri göstereceğiz.
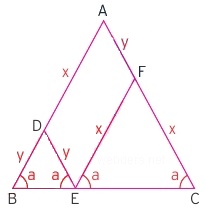
Bir ikizkenar üçgenin tabanından eş olan kenarların her birine diğer kenara paralel olacak şekilde doğru parçaları çizildiğinde yine ikizkenar üçgenler oluşur. Aslında bunun nedeni de paralellikten gelen yöndeş açıların aynı olmasıdır. Aşağıda bunun mantığı gösterilmiştir.
Yukarıdaki üçgende eşit olan kenarlara bakan açılar a harfi ile gösterilmiştir. Tabandan çizilen doğru parçalarıyla paralellik sağlandığından yine a açısı elde edilmektedir. Bu durumda küçük üçgenler de birer ikizkenar üçgen olmaktadırlar. Bununla ilgili bir soru çözelim.
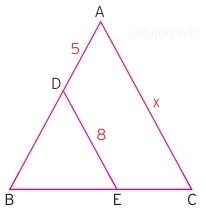
Yukarıdaki üçgende |AB| = |AC| ve |DE| doğru parçası |AC| kenarına paraleldir. Bu durumda x uzunluğu kaç birim olur?
Çözüm: |DE| doğru parçası paralel çizildiği için küçük üçgende ikizkenar olur. Bu durumda |DB| = |DE| = 8 olur. |AB| = 8 + 5 = 13 olur. |AC| = |AB| = 13 bulunur.
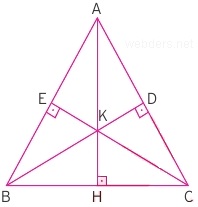
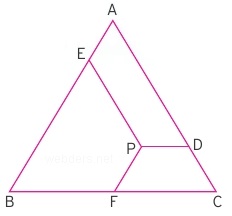
İkizkenar üçgende eş kenarlara indirilen dikme uzunlukları da eşit olmaktadır.
Yukarıdaki üçgende |BE| = |DC|, |EK| = |DK|, |AE| = |AD|, |BK| = |CK| eşitlikleri vardır. |AH| dikmesi eş kenarlar arasında simetri ekseni vazifesi görmektedir.
İkizkenar Üçgende Soru Çözme Yöntemleri
İkizkenar üçgen sorularını hem kenar uzunluğu açısından hem de açı ölçüsü açısından çözmek için dikkat etmeniz gereken bazı hususlar bulunmaktadır. Öncelikle sorularda kolaylık sağlamak için mutlaka eşit kenarları belirtmeniz gerekir. Bunu eşit kenarlara aynı işareti koyarak gerçekleştirebilirsiniz. Bazı sorularda bu işaretler zaten bulunmaktadır.
Soruları çözerken YAK ı asla unutmayın. YAK açılım olarak yükseklik, açıortay ve kenarortay manasına gelir. İkizkenar üçgenin eşit kenarlarının birleştiği köşeden çizilen bu doğru parçası sihirlidir. Üç özelliği de birlikte gösterip sorunun kolaylığını sağlar. Eğer yapacak hiçbir şey bulamıyorsanız ilk yapmanız gereken bunu çizmektir. Bazen doğru parçasını size verir ve yükseklik olduğunu söyler. Buradan açıortay ve kenarortay olduğunu kendiniz çıkarmalısınız. Bunlara dikkat edildiği halde bu konuya ait sorular rahatlıkla çözülecektir.
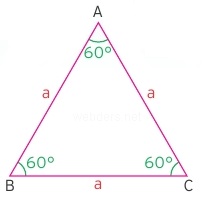
Eşkenar Üçgen
Üç kenarının uzunluğu da eşit olan üçgene eşkenar üçgen denir. Kenarların hepsinin eşit olması açıların hepsinin de eşit olmasını beraberinde getirir. Üçgenin iç açıları toplamı 180 derece olduğuna göre eşkenar üçgenin her bir açısı 60 derecedir sonucuna varabilir. Eşkenar üçgen öğrenciler tarafından çok sevilen bir üçgen tipidir. Çok fazla eşitlik olması işlemleri kolaylaştırır ve bizi kolay hedefimize götürür. Kısacası eşkenar üçgen en düzgün üçgendir diyebiliriz.
İkizkenar üçgen için geçerli her özellik eşkenar üçgende de aynen geçerli olacaktır. Çünkü eşkenar üçgende de iki eşit kenar bulunur. Ekstradan sadece diğer kenar da eşittir. Dolayısıyla üçgen içerisinde indirilen dikmenin hem yükseklik hem açıortay hem de kenarortay olması burada da geçerlidir.
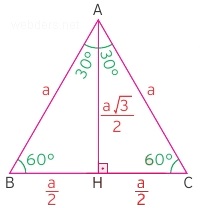
Eşkenar Üçgenin Yüksekliği
Üçgende yükseklik çizdiğimiz zaman üçgenin temel özelliklerini de elde etmiş oluruz. Bu nedenle eşkenar üçgenin yüksekliği önemlidir. Yükseklik bize kenarlar arasındaki oranları da verecektir.
Eşkenar bir üçgenin her bir kenarına a birim dersek. Yükseklik de a nın yarısın √3 katı olacaktır. Ortaya aynı zamanda 30- 60 – 90 üçgeni de çıkacaktır. Tamamen simetrik ve özellikleri belirlenmiş bu üçgende yüksekliği hangi köşeden çizerseniz çizin sonuç değişmeyecektir.
Yukarıdaki şekli iyice zihninize oturttuğunuz taktirde eşkenar üçgen sorularında hiçbir problem yaşamazsınız. Aslında böyle bir görünüm bu konuyu özetlemektedir.
Eşkenar üçgende işlem yapmaya başlamadan önce her açının 60 derece olduğunu belirtmek için açıları üçgen içerisine yazın. Bunu yaptığınızda bir şeyleri gözden kaçırmanız daha zor hale gelecektir.
Soru: Yüksekliği 2√3 cm olan eşkenar üçgenin çevresi kaç cm dir?
Çözüm: Yükseklik bir kenar uzunluğunun yarısının √3 katı kadardır. Bu durumda bir kenar 4 cm olacaktır. Üçgenin çevresi de 4×3 = 12 cm olacaktır.
Eşkenar Üçgende Yardımcı Özellikler
Eşkenar üçgende yardımcı birçok özellik bulunmaktadır. Bu özelliklerin birçoğu birbiri ile doğrudan bağlantılı olduğu için hepsinin üzerinde durmayacağız. Zaten ikizkenar üçgende geçerli olan her şey eşkenar üçgen için de geçerlidir.
Çözüm: Paralel doğru parçalarının toplamı bir kenarın uzunluğuna eşittir. Buna göre bir kenar uzunluğu 3 + 4 +5 = 12 olur. Üçgenin çevresi ise 3.12 = 36 birim olur.
Özel Üçgen Soruları
Açılarından biri 30°, 45°, 60°, 120°, 135° ve 150° olan üçgenleri özel üçgenler olarak isimlendiriyoruz. Bu üçgenlerle ilgili olan soruları çözerken 30°- 60° – 90° ve 45° – 45° – 90° üçgenlerinin kenar özelliklerinden faydalanırız. Eğer açımız 30°, 45° veya 60° gibi dar bir özel açı ise, açının karşısına dikme inerek, 120°, 135° veya 150° gibi bir geniş açı ise, açının bütünlerini oluşturduktan sonra dış açının kollarından birine dikme ineriz. Daha sonra Pisagor teoremini uygulayarak çözüme gideriz.