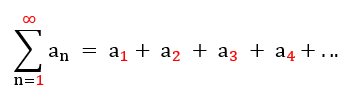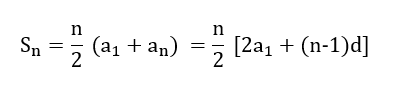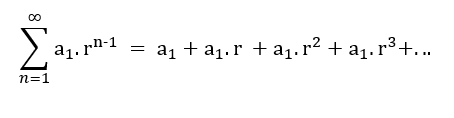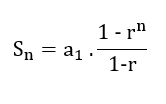Seriler Konu Anlatımı: Aritmetik ve geometrik serilerin temellerini, toplama yöntemlerini ve bu serilerin matematiksel analizdeki uygulamalarını öğrenin.
Seriler
- (an) reel terimli bir dizi olsun.
sonsuz toplamına seri denir. an’e serinin genel terimi denir.
Serinin ilk n teriminin toplamından oluşan Sn = a1+a2+a3+ …+an toplamına serinin n. kısmi toplamı denir. (Sn) = (S1,…,S2,…,S3,…,Sn,…) dizisine kısmi toplamlar dizisi denir.
a) (Sn) dizisi yakınsak ise
serisi de yakınsaktır ve serinin toplamı
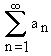
b) (Sn) dizisi ıraksak ise
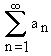
serisi yakınsak ise lim an = 0’dır. Bu ifadenin tersi doğru değildir. Yani, lim an = 0 iken
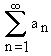
lim an≠0 ise
serisi ıraksaktır.
Serileri iki grupta inceleriz:
Aritmetik Seri
Eğer (an) bir aritmetik dizi ise, bu dizinin elemanlarının toplanmasıyla aritmetik dizi oluşacak demektir.
Aritmetik serilerde ilk n terimin toplamı bulunabilir. Bu, kısmi toplam olarak adlandırılır ve genelde Sn ile gösterilir. Her bir dizi elemanı arasında d kadar fark olan bir aritmetik seride toplamı hesaplamak için formül kullanırız. Aritmetik seri toplam formülü:
Yani ilk n terimin toplamı bulunurken, ilk terim ve n. terimi toplayıp toplam terim sayısının yarısına bölmen beklenir. (İlk terim + n. terim) ifadesi yerine, son terimi de ilk terim cinsinden yazıp formülü sadece ilk terim cinsinden ifade edebilirsin.
Geometrik Seri
Eğer (an) bir geometrik dizi ise, bu dizinin elemanlarının toplanmasıyla geometrik dizi oluşacak demektir. Geometrik dizileri, önceki elemanı r ile çarparak oluşturuyorduk. Yani geometrik serileri aşağıdaki gibi ifade edebiliriz:
Geometrik serilerde de ilk n terimin toplamı yani kısmi toplam bulunabilir. Elemanlar, r ortak çarpanına sahiptir. Geometrik seri toplam formülü: