Geometrik dönüşümleri keşfedin: ‘Dönüşümlerle Geometri Konu Anlatımı’ ile şekillerin evrimini ve matematiksel güzelliklerini öğrenin!
YANSIMA
YANSIMA HAREKETLERİ:
- Yansıma hareketlerinde şeklin boyutu değişmez.
- Yansıma hareketlerinde şeklin yönü ve yeri değişir.
- Yansıma hareketlerinde şeklin tam simetrisi meydana gelir.
- Yansımaya en güzel örnek kişinin aynadaki görüntüsüdür.
YANSIMA HAREKETLERİNİN KOORDİNAT DÜZLEMİNDEKİ DEĞİŞİMİ:
- Yansıma hareketimiz eğer X eksenine göre yansıtılıyorsa, şeklin X eksenindeki koordinat değeri aynen kalır.
- Yansıma hareketimiz eğer Y eksenine göre yansıtılıyorsa, şeklin Y eksenindeki koordinat değerinin işareti değişir.
- Yansıma hareketimiz orijine göre yansıtılıyorsa, hem X hem de Y eksenlerinin koordinatlarının işaretleri değişir.
- Yansıma hareketlerinde eğer şeklimizin herhangi bir köşesi noktasında yani orijin üzerinde ise, bu köşenin bulunduğu yer değişmez.
NOT:
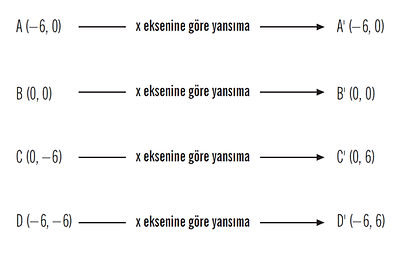
*Bir noktanın x eksenine göre yansıması alınırken noktanın y koordinatının işareti değişir, x koordinatı aynen kalır.
Bu durum cebirsel olarak,
(x, y) -> (x, –y) şeklinde gösterilir.
*Bir noktanın y eksenine göre yansıması alınırken noktanın x koordinatının işareti değişir, y koordinatı aynen kalır.
Bu durum cebirsel olarak,
(x, y) -> (–x, y) şeklinde gösterilir.
Örnek:
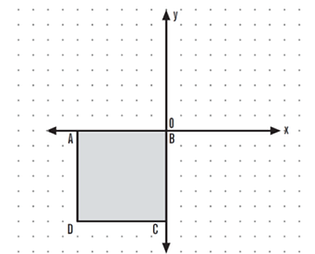
Köşe noktaları A(–6, 0), B(0, 0), C(0, –6) ve D(–6, –6) olan ABCD dörtgeninin x eksenine göre yansıması A’B’C’D’ dörtgenidir. ABCD ve A’B’C’D’ dörtgenlerini çizimle gösteriniz.
ÖTELEME
ÖTELEME HAREKETLERİ
- Öteleme hareketlerinde, şeklin yönü, boyutu değişmez.
- Öteleme hareketlerinde, şeklin bulunduğu yer değişir.
- Öteleme Hareketlerinde Koordinatların Değişimi:
- Öteleme hareketlerinde, x eksenine göre sağa veya sola öteleme hareketi yapılır.
- Sağa göre yapılan öteleme hareketinde x koordinatına öteleme miktarı eklenir ve y koordinatı aynen yazılır.
- Sola göre yapılan öteleme hareketinde x koordinatından öteleme miktarı çıkartılır ve y koordinatı aynen yazılır.
- Öteleme hareketlerinde, y eksenine göre yukarı ya da aşağı öteleme hareketi yapılır.
- Yukarı yönlü yapılan öteleme hareketinde, y koordinatına öteleme miktarı eklenir ve x koordinatı aynen yazılır.
- Aşağı yönlü yapılan öteleme hareketinde, y koordinatından öteleme miktarı çıkarılır ve x koordinatı aynen yazılır.
- Hem sağ-sol öteleme hareketinde hem de yukarı-aşağı öteleme hareketinde, eğer her iki çeşit öteleme aynı anda yapılıyorsa, ötelemenin yönüne göre x ve y koordinatlarına ekleme ya da çıkarma aynı anda yapılır.
NOT:
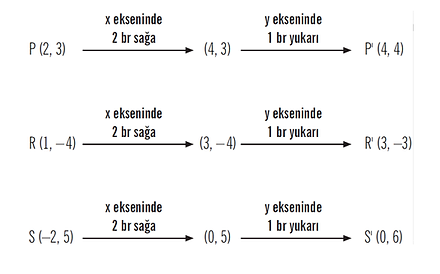
*x eksenine göre yapılan ötelemelerde sağa doğru ötelemede x değeri öteleme miktarı kadar arttırılır, sola doğru ötelemede x değeri öteleme miktarı kadar azaltılır. Y değeri değişmez.
*y eksenine göre yapılan ötelemelerde yukarı doğru ötelemede y değeri öteleme miktarı kadar arttırılır, aşağı doğru ötelemede y değeri öteleme miktarı kadar azaltılır. X değeri değişmez.
Örnek:
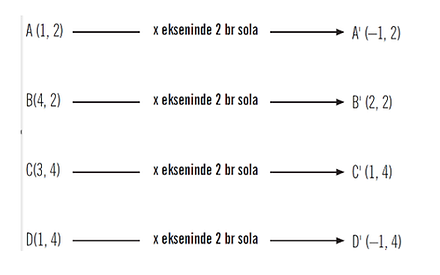
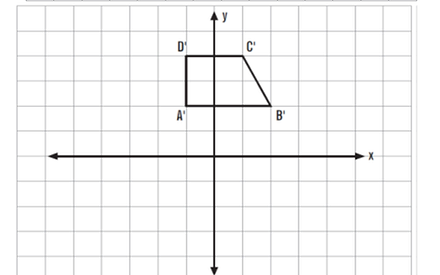
Örnek:
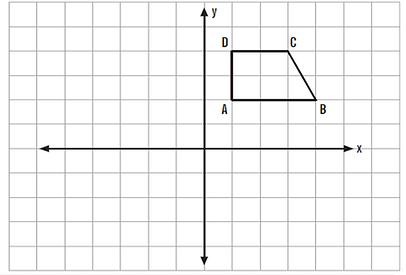
Aşağıda verilen ABCD yamuğunun x ekseninde 2br sola ötelenmiş görüntüsünü çizelim.
DÖNDÜRME
DÖNME HAREKETLERİ
- Dönme hareketlerinde, şeklin büyüklüğü değişmez.
- Dönme hareketlerinde, şeklin yönü değişir.
- Dönme hareketlerinde, şeklin yeri değişir.
- Dönme hareketlerimizde 180’lik dönme şekli ilk konumuna getirir.
- Dönme hareketlerimizde 360’lik dönme şeklin yansıması ile aynı hareketi verir.
Dönme Hareketlerinde Koordinat Düzlemindeki Değişimler:
- Dönme hareketlerimizde her 90’’lik dönme x,y koordinatlarının yerini değiştirir.
- Dönme hareketlerinde yer değiştiren x,y koordinatlarının işaretlerini bulunduğu bölgeye göre biz belirleriz.
- Dönme hareketlerinde, hareket yönümüz saat yönüne göre veya saatin tersi yönüne göre yapılır.
- Sonuç olarak bir şeklin koordinatları yer değişir ve bulunduğu bölgeye göre işaretlerini yerleştiririz.
NOT: Koordinatlarından biri (a, b) olan bir şekil, orijin etrafında saatin dönme yönünde;
*90° döndürüldüğünde (a, b) koordinatları (b, –a),
*180° döndürüldüğünde (a, b) koordinatları(–a, –b) olur.
*360° döndürüldüğünde ise (a, b) koordinatları değişmez.
Örnek:
Örnek:
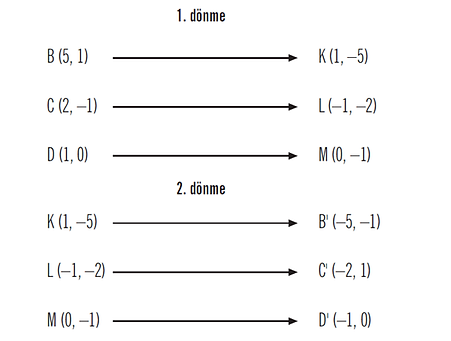
BCD üçgeninin köşe noktalarının koordinatları B(5, 1), C(2, 1) ve D(1, 0)’dır.
BCD üçgeni orijin etrafında saatin dönme yönünde en az kaç derecelik açı ile döndürülürse oluşan B’C’D’ üçgeninin koordinatları B'(–5, –1), C'(–2, 1) ve D'(–1, 0) olur?
Çözüm:
BCD üçgenini saatin dönme yönünde 90° döndürelim.
BCD üçgeni 2. defa saatin dönme yönünde 90° döndürüldüğünde B’C’D’ üçgeninin köşe noktalarının koordinatları elde edildi. Buna göre BCD
Üçgeni orijin etrafında 180° lik açıyla döndürülmelidir.