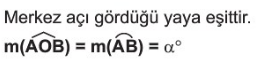Çember ve Daire Konu Anlatımı

Çember ve Daire Konu Anlatımı ile bu temel geometrik şekillerin özelliklerini, formüllerini ve uygulamalarını ayrıntılı bir şekilde öğrenin!

Çember

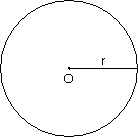
Düzlemde sabit olan bir noktadan eşit uzunluktaki noktaların oluşturduğu kümeye çember denir.

O noktası çemberin merkezi olmak üzere ;

yarıçap=r=|QA|=|OB|

çemberin çapı=|AB|

|AB| =2r’dir.

 

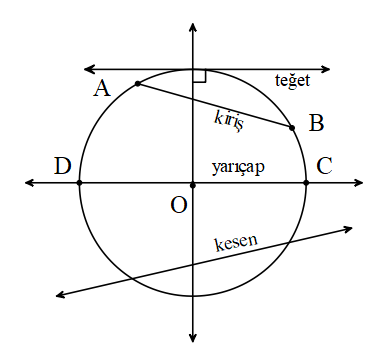
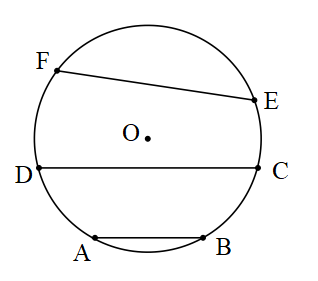
Çemberin Elemanları

Düzlemde sabit bir noktaya (merkez) eşit uzaklıkta (yarıçap) bulunan noktalar kümesine çember denir.

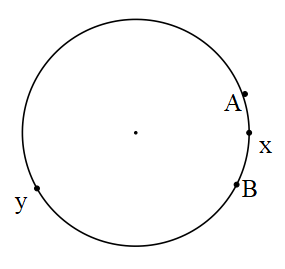
Yay: Bir çember üzerindeki farklı iki nokta arasında kalan çembere ait noktalar kümesine çember yayı denir.

A ve B noktaları arasındaki yaylar AxB ve AyB yaylarıdır.

 

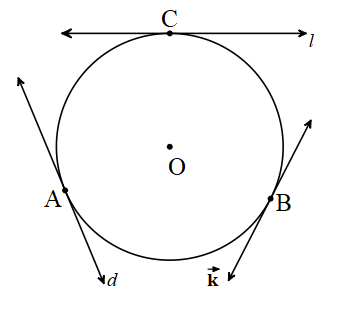
Teğet: Bir çember ile tek bir ortak noktası olan doğruya çemberin bir teğet doğrusu denir.

d,k,l O merkezli çemberin herhangi üç teğet doğrusudur.

 

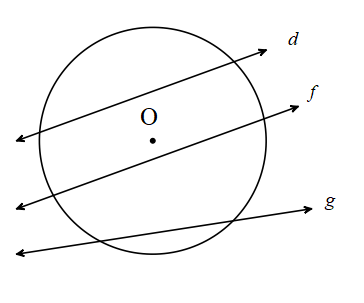
Kesen: Çemberi farklı iki noktada kesen doğruya çemberin keseni denir.

d,e,f doğruları O merkezli çemberin kesenleridir.

 

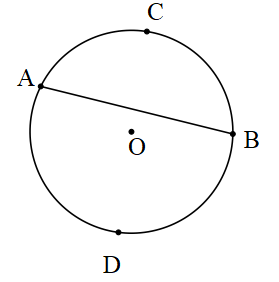
Kiriş: Bir çemberin farklı iki noktasını birleştiren doğru parçasına çemberin kirişi denir.

[AB], [DC], [EF] doğru parçaları O merkezli çemberin kirişleridir.

 

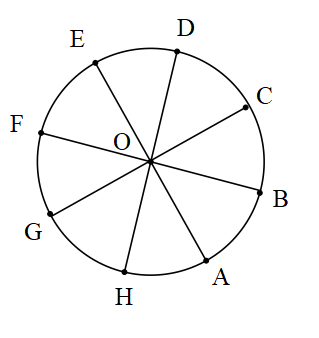
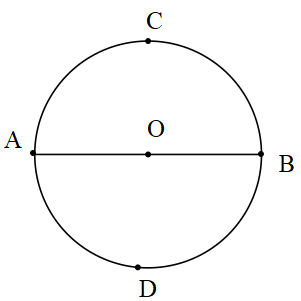
Çap: Merkezden geçen kirişe çap denir.

[AE],[BF],[CG],[DH] doğru parçaları O merkezli çemberin çap doğrusudur. Bu doğruların uzunlukları çemberin çap uzunluğu olur.

 

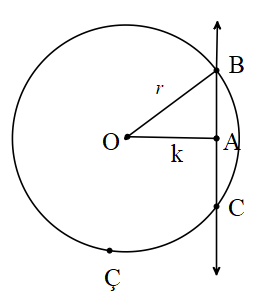
Bir Düzlemde Bir Çember ile Bir Doğrunun Birbirlerine Göre Durumları

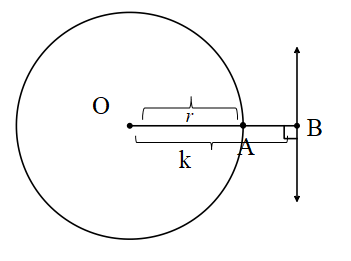
Doğru çemberi kesmez

O noktasından doğruya olan uzaklık (dik) yarıçaptan büyük ise doğru ile çember kesişmez.

[OB] ⊥ d, |OA|=r, |OB|=k

k>r ise d∩ Ç= {} olur.

 

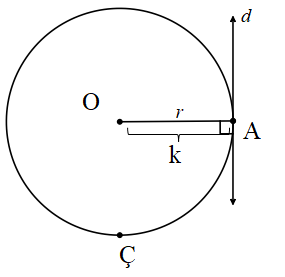
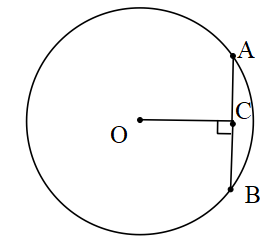
2. Doğru çembere teğet olur.

Çemberin merkezinin d doğrusuna olan uzaklığı yarıçapa eşit olduğunda “çeber doğruya teğettir” denir. Çember ile doğrunun bu durumda tek bit ortak noktası (A) olur.

[OA] ⊥ d, |OA|=k

k=r ise d∩ Ç= {A} olur.

 

3.Çember ile doğru farklı iki noktada kesişir.

Çember merkezinden doğruya olan uzaklık çemberin yarıçapından küçük ise doğru çemberi iki farklı noktada keser.

[OA] ⊥ d, |OA|=k |OB|=k

r>k ise d∩ Ç= {B,C} dir.

 

Çemberde Kirişin Özellikleri

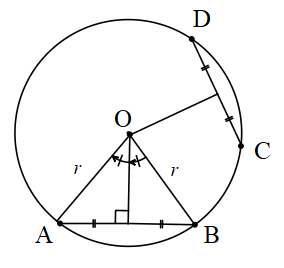
1. Bir çemberin merkezinden herhangi bir kirişe çizilen dik doğru kirişi iki eş parçaya ayırır.

[OC] ⊥ [AB] ⇔ |AC|=|CB|

bu durumda AOB üçgeni ikizkenar üçgen olur.

 

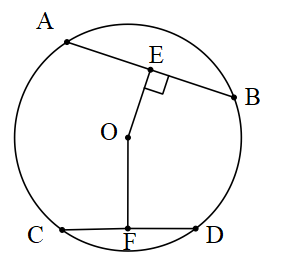
2. Bir çemberde eşit uzunluktaki kirişlerin çemberin merkezine olan uzaklıkları eşittir.

|AB|=|CD| ⇔ |OE|=|OF|

 

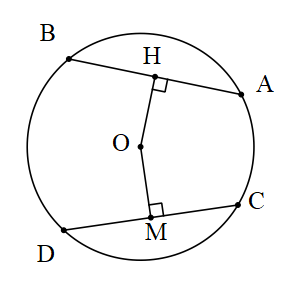
3. Bir çemberde kiriş merkeze yaklaştıkça uzunluğu artar.

 

|OH|>|OM| ⇔ |AB|=|CD|

 

Çemberde Açı Çevrel Çember ve Sinüs Teoremi

Çemberin iki noktası arasında kalan çember parçasına yay denir.

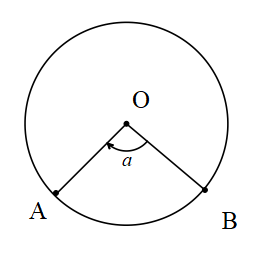
Merkez Açı

O merkez [OA ve [OB ışın AOB açısının gördüğü yay AB yayıdır.

 

Çevre Açı

Köşesi çember üzerinde ve kenarları çember kirişi olan açıya çevre açı denir.

O merkez [AB] ve [BC] çember krişi B oktası çember üzerinde ve ABC açısının köşesidir.

Çevre açı gördüğü yayın ölçüsünün yarısına eşittir.

 

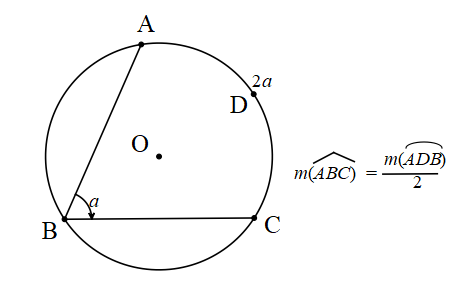
Teğet-Kiriş Açı

Bir çemberde teğet doğrusu ile kiriş arasında kalan açıya teğet kiriş açı denir. A noktası çember ile doğrunun ortak teğet noktasıdır.

Teğet-kiriş açı aynı zamanda çevre açı olduğundan gördüğü yayın yarısına eşittir.

 

Çemberde İç Açı

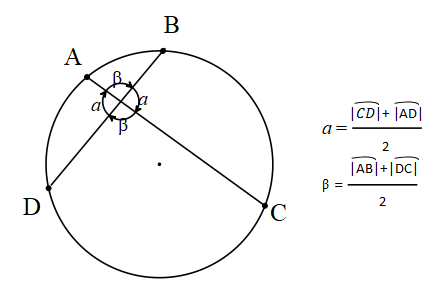
[BD] ∩[AC]={K} çemberde kesişen iki kirişin oluşturduğu açıya iç açı denir.

 

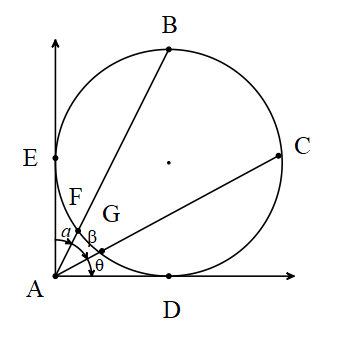
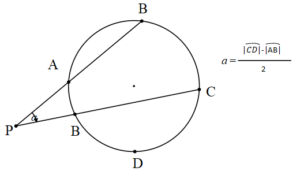
Çemberde Dış Açı

Köşesi (a) çemberin dış bölgesinde olan iki kesenin iki teğetin veya bir teğet ile bir kesenin oluşturduğu açıya dış açı denir.

a,β,θ birer dış açıdır.

Çemberde dış açı gördüğü çember yayların farkının yarısıdır.

 

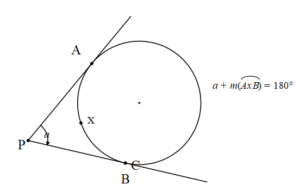
Teğetler Arasında Kalan Dış Açı

A ve B teğet noktalarıdır. APB açısı teğetler arasında kalan açıdır. Bu açı aynı zamanda bir dış açıdır.

Teğetler arasında açı ile bu açının gördüğü küçük yayın toplamı 180º’dir.

 

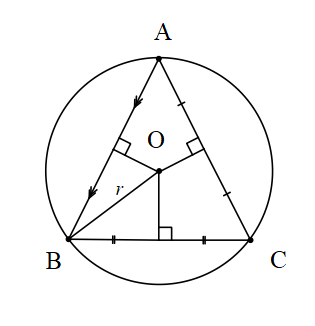
Bir Üçgenin Çevrel Çemberi

O merkezli r yarıçaplı çember ABC üçgeninin çevresel çemberidir.

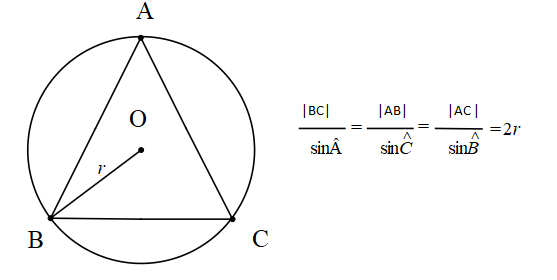
Sinüs Teoremi

Bir ABC üçgeninin çevrel çemberinin yarıçapı r olmak üzere;

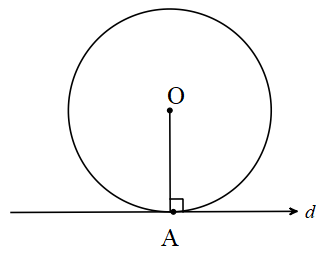
Çemberde Teğet

Bir çembere herhangi bir noktadan çizilen teğet değme noktası olan A’da yarıçapa diktir.

[OA] ⊥ d

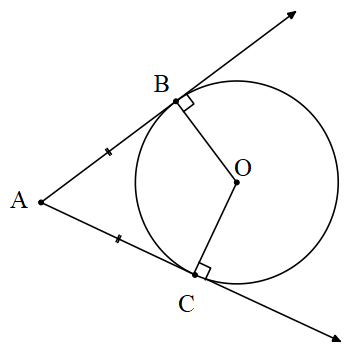
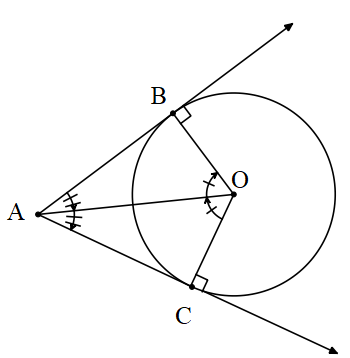
1. Bir çembere dışındaki bir noktadan çizilen teğet uzunlukları eşittir.

Bir çembere dışındaki bir noktadan çizilen teğetlerin arasında kalan ve çemberi gören açının açıortayı çemberin merkezinden geçer.

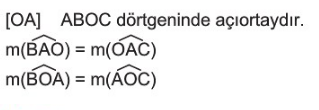
2. İç Teğet Çember

ABC üçgeninde açıortayların kesim noktası iç teğet çemberin merkezi olur.

 

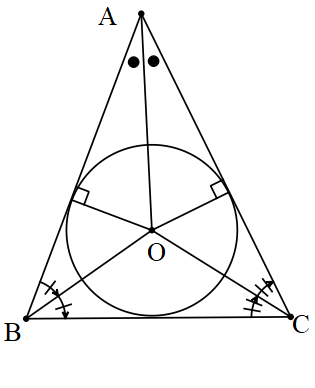
3. Dış Teğet Çember

İki dış açının açıortaylarının kesim noktası üçgenin dış teğet çemberinin merkezidir. Şekilde O1, O2, O3 noktaları ABC Üçgeninin dış teğet çemberlerinin merkezleridir.

Dairede Alan ve Uzunluk

O merkezli ve r yarıçaplı bir dairede

Dairenin Alanı= π x r²

Dairenin Çevresi = 2πr

 

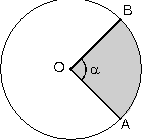
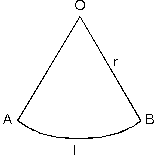
Daire Diliminin Alanı ve Yay Parçasının Uzunluğu

O merkezli dairede m(AOB) = a olacak şekilde taralı daire diliminin alanı,

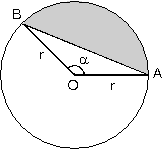
Daire Kesmesinin Alanı

O merkezli dairede taralı alan, daire diliminin alanından BOA üçgeninin alanının çıkarılması ile bulunur.

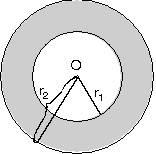
Daire Halkasının Alanı

O merkezli r1 ve r2 yarıçaplı çemberler arasındaki dairenin alanının çıkarılması ile bulunur. Taralı Alan=pr₂² – pr₁²p ortak parantezinde

Taralı Alan =p(r₂² – r₁²)

 

O merkezli ve r yarıçaplı daire diliminde yay uzunluğuna

|AB| = l dersek