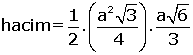Katı Cisimler Konu Anlatımı ile üç boyutlu geometriyi keşfedin. Küplerden silindirlere, geometrik şekillerin hacim ve yüzey alanlarını öğrenin!
PİRAMİTLER
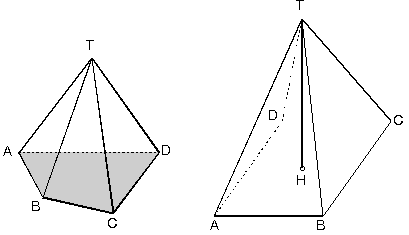
Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir.
T noktası piramidin tepe noktasıdır. Kapalı bölge ise piramidin tabanıdır. Piramit; tabanı oluşturan şeklin ismiyle adlandırılır. Taban kare ise, kare piramit; taban altıgense altıgen piramit gibi.
Eğer piramidin tabanı düzgün çokgense bu tip piramitlere düzgün piramit denir.
T noktasının taban düzlemi üzerindeki dik izdüşümüne H dersek [TH] piramidin yüksekliği olur.
|TH| = h biçiminde yazılır. [TA], [TB], [TC]… piramidin yanal ayrıtlarıdır.
Piramitlerin hacmi taban alanı ile yüksekliğin çarpımının üçte biri kadardır.
Düzgün Piramit Hacim Hesabı
Kare Piramit
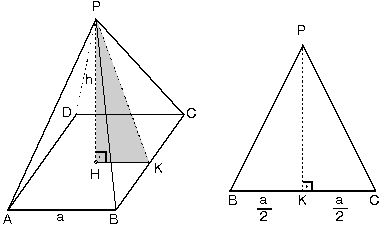
Kare piramidin tabanı kare biçimindedir. Yan yüzeyleri ise dört adet ikizkenar üçgenden oluşur.
İkizkenar üçgenlerin taban uzunlukları piramidin tabanının bir kenarına eşittir.
|PH| = h piramidin yüksekliğidir.
Yan yüz yüksekliği |PK| dır.
Tabanının bir kenarına a dersek
Buradan yan yüz yüksekliği
|PK|2 = h2 + (a/2 )2 olur.
Tüm alan yan yüz alanları ile taban alanının toplamına eşittir.
Eşkenar Üçgen Piramit
Tabanı eşkenar üçgen olan piramitlere eşkenar üçgen piramit denir.
Düzgün Dörtyüzlü
Dört yüzü de eşkenar üçgenlerden oluşan cisimdir. Yükseklik, tabanı oluşturan üçgenin ağırlık merkezine iner.
Bir ayrıtı a olan düzgün dörtyüzlünün
Yarı yüz yüksekliği ve
Cisim yüksekliği olur
Buradan
Düzgün Sekizyüzlü
Bütün ayrıtları birbirine eş ve yüzeyleri sekiz eşkenar üçgenden oluşan cisme düzgün sekizyüzlü denir. Bir ayrıtına a dersek yan yüz yüksekliği olur. Cismin, ortak tabanlı iki adet kare piramitten oluştuğunu düşünürsek piramitlerin yüksekliği;
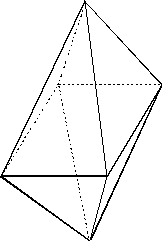
Piramitin hacmi olduğundan;
Yüzey şekilleri eşkenar üçgen olduğundan
Düzgün Altıgen Piramit
Tabanı düzgün altıgen olan piramide düzgün altıgen piramit denir. Yan yüzeyleri altı adet eş ikizkenar üçgenden oluşur.
Taban alanı = olduğundan
bulunur. Yan yüzeyleri altı adet eş ikizkenar üçgen oluşur.
KONİ
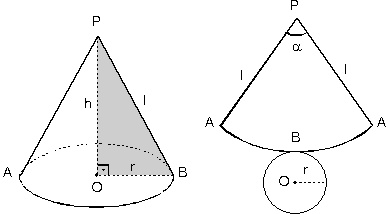
Tabanı daire biçiminde olan piramite koni adı verilir. Burada; Taban yarıçapı |OB| = r
Cisim yüksekliği |PO| = h olur.
|PA| = |PB| = l uzunluğuna ana doğru denir.
POB dik üçgeninde,
h2 + r2 = l2 bağıntısı vardır. Koninin yanal alanı bir daire dilimidir.
Koni Hacim Hesabı
Daire diliminin alanı, yay uzunluğu ile yarıçapın çarpımının yarısıdır. Yay uzunluğu taban çevresine eşit olduğundan,
Koni Yanal Alan Hesabı
Yanal alan= πr2+πrl
Tüm alan bulunurken, taban alanı da ilave edilir.
Koni Alan Hesabı
Tüm alan = šr2 + šrl
- Daire diliminin merkez açısına a dersek
oranı elde ederiz.
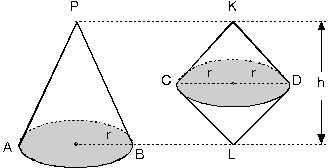
Yükseklikleri ve taban yarıçapları eşit olan iki cismin hacimleri de birbirine eşittir.
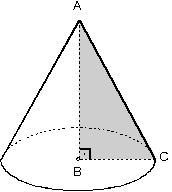
Üçgensel şekiller bir kenarı etrafında döndürüldüğünde koni elde edilir.şekildeki ABC dik üçgeninin AB kenarı etrafında döndürülmesi ile |BC| yarıçaplı ve yüksekliği |AB| olan koni elde edilir.
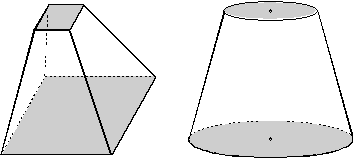
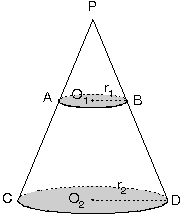
Kesik piramitlerin hacimleri bulunurken cisim piramide tamamlanır.
[O1B] // [O2D] olduğundan
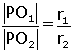
Küçük koninin büyük koniye benzerlik oranı dir. Alanları oranı benzerlik oranının karesi olduğundan, alanlar oranı
olur.
KÜRE NEDİR?
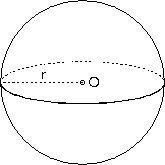
Uzayda bir noktadan eşit uzaklıktaki noktaların geometrik yerine küre yüzeyi denir. Küre yüzeyinin sınırladığı cisme küre adı verilir. Sabit noktaya kürenin merkezi, merkezin küre yüzeyine uzaklığına da kürenin yarıçapı denir.
O merkezli R yarıçaplı kürede;
KÜRE HACİM FORMÜLÜ
KÜRE YÜZEY ALAN FORMÜLÜ
Yüzey alanı:
-
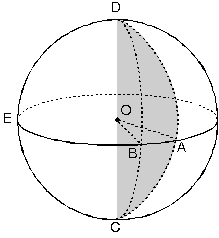
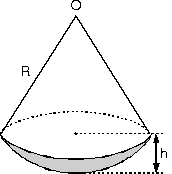
Küre Dilimi
[KL] çap
m(AOB) = a
şekildeki gibi kesilip çıkarılan küre diliminin hacmi
-
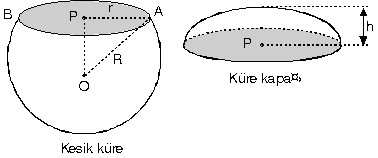
Küre Kapağı
Bir küre merkezinden |OP| uzaklıkta bir düzlemle kesildiğinde kesit alanının daire şeklinde olduğu görülür.
Kesilip çıkarılan kısma küre kapağı denir. Kesitin merkezinden uzaklığına |OP|, kesitin yarıçapına r ve kürenin yarıçapına R dersek
|OP|2 + r2 = R2 eşitliği vardır. h = R –|OP|
Küre kapağının alanı= 2πRh
Yukarıdaki şekildeki gibi olan
Küre parçasının hacmi: 2πR2H
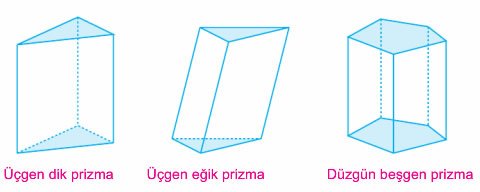
Prizmalar
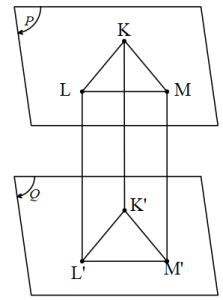
Birbirine paralel P ve Q düzlemleri içerisinde alınan iki eş çokgensel bölgenin tüm noktalarının karşılıklı olarak birleştirilmesiyle elde edilen içi dolu cisme prizma denir.
[K’L’], [K’M’], [L’M’] taban ayrıtlarıdır.
[KK’], [LL’], [MM’] ise prizmanın yanal ayrıtlarıdır.
K’L’M’ üçgeni prizmanın alt tabanı, KLM üçgeni prizmanın üst tabanı, KLL’K’, KMM’K’, LMM’L’ dörtgensel bölgeleri de prizmanın yanal alanıdır. Eğer bir prizmada yanal ayrıtlar taban düzlemine dik iniyorsa bu prizmaya dik prizma denir. Dik olmayan prizmalara ise eğik prizma denir. Alt ve üst taban düzlemleri arasındaki uzaklığa prizmanın yüksekliği denir.
Prizmalar, tabanına göre isim alır. Tabanı kare ise kare prizma, tabanı üçgen ise üçgen prizma, tabanı daire ise silindir denir.
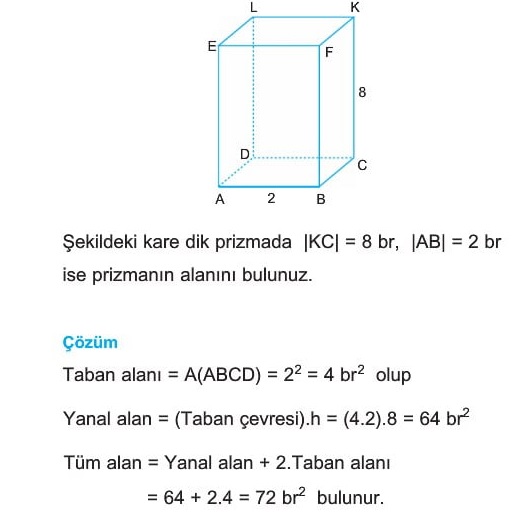
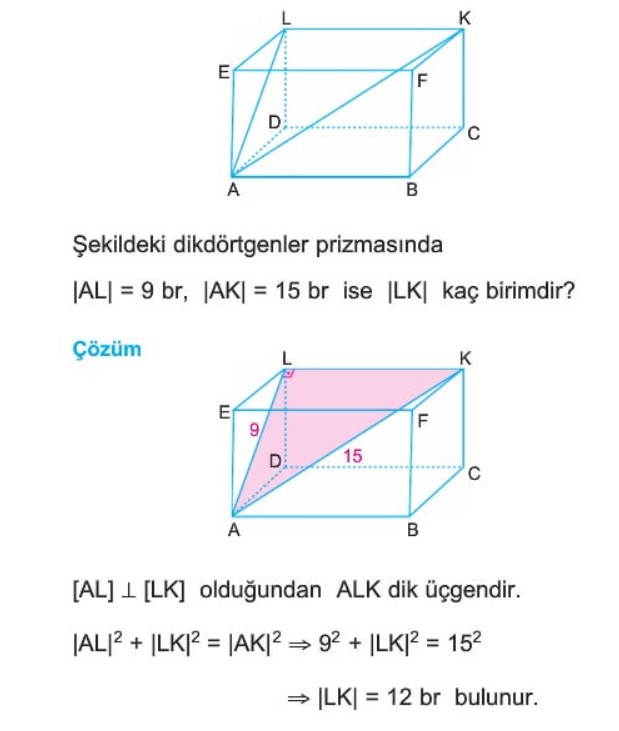
Örnek:
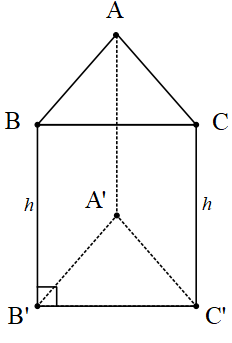
Dik Prizmalar
Yukarıdaki şekilde [AA’], [BB’] ve [CC’] yanal ayrıtları alt ve üst tabanlara diktir. Bu yüzden bu prizma bir üçgen dik prizmadır. Alt ve üst tabanlar özdeş olduğu için alanları eşittir. Yanal yüzler dikdörtgendir.
Y.A. = Taban çevresi x Cisim Yüksekliği
Y.A = Ç(A’B’C’) x h
Prizmanın alanı ise tüm yüzeylerinin alanları toplamıdır.
Prizmanın alanı= taban alanı+yanal alanı
Prizmanın alanı= 2A(ABC)+Ç(A’B’C’). h
Dik Prizmanın hacmi ise Taban Alanı x Yükseklik bağıntısı ile bulunur.
V = Taban Alanı x Yükseklik
V=S.h
Örnek:
Küp
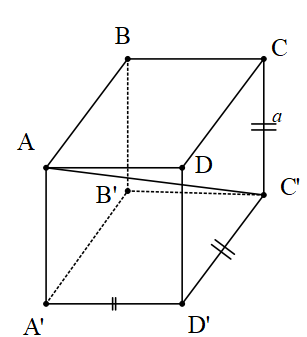
Tüm ayrıtları eşit uzunlukta olan dikdörtgen prizmalara küp denir. Yüzey köşegeni = a√2 dir.
*6 tane yüzey vardır ve yüzeylerin tamamı karedir.
*Her biri eşit uzunlukta 12 tane ayrıtı vardır.
*Küp içerisinde birbirine en uzak iki köşe arasındaki doğru parçasına cisim köşegeni denir.
*Yukarıda çizilen küpün cisim köşegenleri [AC’], [BD’], [CA’] ve [DB’] dür. Cisim köşegenleri eşit uzunluktadır.
Bir ayrıtı a cm olan yukarıdaki küpte,
** Cisim köşegeni uzunluğu |AC’| = a√3 cm
** Küpün alanı A = 6a2
** Küpün hacmi v = a3‘tür.
Örnek:
Örnek:
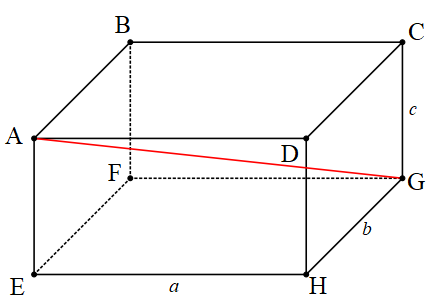
Dikdörtgenler Prizması
Ayrıt uzunlukları a,b ve c cm olan şekildeki dikdörtgenler prizmasının tüm yüzeyleri dikdörtgendir.