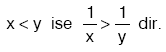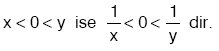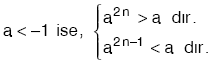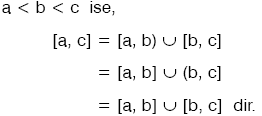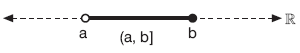Sıralama Konu Anlatımı

Sıralama Konu Anlatımı ile matematiksel düzen ve mantığı öğrenin. Nesnelerin ve kavramların sıralanması, permütasyon ve kombinasyon temelleri burada!

Sıralama

1. TANIM

a, b ye eşit değilse, “a ≠ b” biçiminde yazılır. a ≠ b ise bu durumda; a > b, “a büyüktür b den” ya da a < b, “a küçüktür b den” olur.

Gerçel (reel) sayı ekseninde herhangi bir sayının sağında bulunan sayılar daima o sayıdan büyük, solunda bulunan sayılar da o sayıdan küçüktür.

Yukarıdaki sayı doğrusuna göre; a < b < c dir.

x > y,  x ≥ y,  x < y ve x ≤ y şeklindeki ifadelere eşitsizlik denir.

SIRALAMANIN ÖZELİKLERİ

x, y, a, b reel (gerçel) sayılar olmak üzere,

Bir eşitsizliğin her iki tarafına aynı sayı eklenebilir veya çıkarılabilir.  a < b  ise  a + c < b + c  dir.  a < b  ise  a – c < b – c  dir.

Bir eşitsizliğin her iki tarafı pozitif bir reel sayıyla çarpılır veya bölünürse eşitsizliğin yönü aynı kalır.  a < b  ve  c > 0  ise  a × c < b ×c  dir.  a < b  ve  c > 0  ise dir.

Bir eşitsizliğin her iki tarafı negatif bir reel sayı ile çarpılır veya bölünürse eşitsizlik yön değiştirir.  a < b  ve  c < 0  ise  a × c > b ×c  dir.  a < b  ve  c < 0  ise dir.

Eşitsizliklerde geçişme özeliği vardır.(x < y ve y < z) ise x < z dir.

Aynı yönlü eşitsizlikler, taraf tarafa toplanabilir; fakat çıkarılamaz.(x < y ve a < b) ise x + a < y + b dir.

x ile y aynı işaretli olmak üzere,

x ile y zıt işaretli olmak üzere,

n ∈ N⁺ ve  0 < a < b ise aⁿ < bⁿ  dir.

n ∈ N⁺ ve a < b < 0  olsun.

n çift sayma sayısı ise aⁿ > bⁿ dir.

n tek sayma sayısı ise aⁿ <bⁿ dir.

n ∈ Z⁺– {1} olmak üzere,  a > 1 ise, aⁿ> a  dır.  0 < a < 1 ise, aⁿ< a  dır.•  – 1 < a < 0  ise,  aⁿ > a  dır.

• (0 < a < b ve 0 < c < d) ise,

0 < a × c < b × d

f(x) < g(x) < h(x) eşitsizlik sisteminin çözüm kümesi; f(x) < g(x) eşitsizliğinin çözüm kümesi ile g(x) < h(x) eşitsizliğinin çözüm kümesinin kesişimidir.

a × b < 0 ise  a ile b ters işaretlidir.  a × b > 0  ise  a ile b aynı işaretlidir.

REEL

Kapalı Aralık

a ve b sayıları ile bu sayıların arasındaki tüm reel sayıları içine alan küme, [a, b] veya a ≤ x ≤ b , x ∈ R  şeklinde gösterilir ve bu şekilde tanımlanan aralıklara kapalı aralık denir.

Açık Aralık

a, b ∈ R  ve a < b olsun. [a, b] kapalı aralığının uç noktalarının ikisi de bu aralıktan çıkarılırsa elde edilen yeni aralığa açık aralık denir.

a, b ∈ R ve a < b olsun. [a, b] kapalı aralığının uç noktalarından biri çıkarılırsa elde edilen yeni aralığa yarı açık aralık denir.

[a, b] kapalı aralığından b noktası çıkarılırsa [a, b) veya x ∈ R olmak üzere,

a ≤ x < b yarı açık aralığı elde edilir.

[a, b] kapalı aralığından a noktası çıkarılırsa (a, b] veya x ∈ R olmak üzere, a < x ≤ b yarı açık aralığı elde edilir.

[a, b] aralığının uzunluğu, b – a dır.