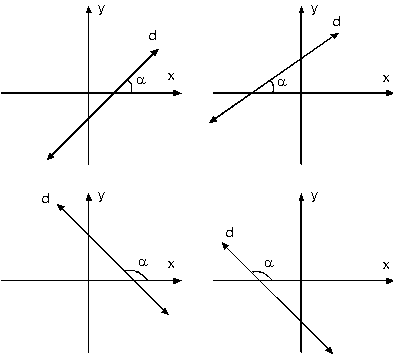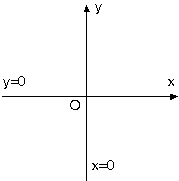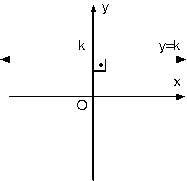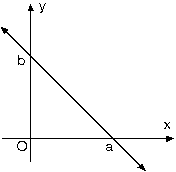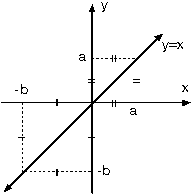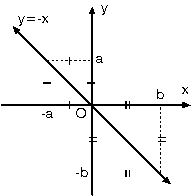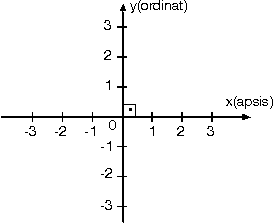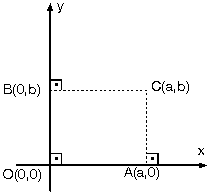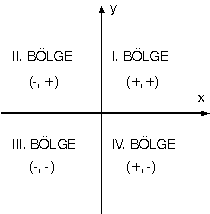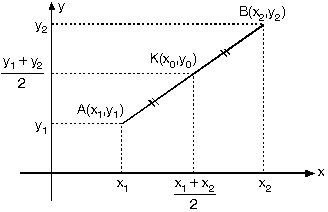Analitik Geometri Konu Anlatımı ile koordinat sistemi üzerinde şekillerin yerini ve özelliklerini anlayın. Geometriyi matematiksel perspektifle keşfedin!
Doğrunun Analitik İncelenmesi
Yukarıdaki şekillerde d doğrusunun farklı durumlarına karşılık oluşan a eğim açısı gösterilmiştir.
Doğrunun denklemi:
Bir doğru üzerindeki noktaların koordinatlarını veren eşitliğe doğrunun denklemi denir.
y = mx + n
y = mx + n eşitliğinde m: eğim, n: sabit sayıdır. ax + by + c = 0 şeklinde verilen denklemde y yalnız bırakılırsa
elde edilir
x in katsayısı eğimi verir.
Öyle ise, ax + by + c = 0 doğrusunun eğimi
Eğimi eşit olan doğrulara paralel doğrular denir. Doğruların eğimleri arasındaki bağıntıdan daha sonra bahsedeceğiz.
İki Noktası Bilinen Doğrunun Eğim ve Denklemi
İki noktası bilinen doğrunun eğimi
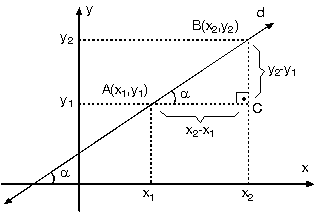
Analitik düzlemde A(x1, y1), B(x2, y2) noktaları bilinen d doğrusu üzerinde A, B noktalarının koordinatları kullanılarak oluşturulan ABC üçgeninin A açısı ile d doğrusunun eğim açısı yöndeş açılar olduklarından eşittirler.
Buradan
olduğundan
şeklinde de yazılabilir
İki noktası bilinen doğrunun denklemi
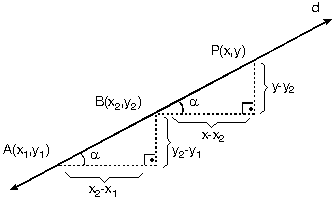
A(x1, y1), B(x2, y2) noktalarından geçen d doğrusu üzerinde doğruyu oluşturan noktaları temsil eden P(x, y) noktası alalım. Bu üç noktadan herhangi ikisini kullanarak yazacağımız eğimler eşittir. Buna göre,
Bu eşitlik bize iki noktası bilinen doğru denklemini verir.
şeklinde de yazılabilir. Sonuç aynıdır.
Orijinden yani O(0,0) noktasından geçen doğrularda x = 0 için y = 0 olacağından
y = mx + n denklemindeki n terimi sıfır olur.
O halde orijinden geçen doğrunun eğimi m ise denklemi y= mx
Doğru denklemi ax + by + c = 0 şeklinde ise ve orijinden geçiyorsa c = 0 dır.
Doğru denklemi ax + by = 0 olur.
Bir Noktası ve Eğimi Bilinen Doğrunun Denklemi
A(x1, y1) noktasından geçen ve eğimi m olan doğru denklemi
A(x1, y1) noktası ve P(x, y) noktası kullanılarak yazılan eğim değeri verilen eğime eşitlenir.
Eksenlere Paralel Doğruların Denklemi
a. Eksen doğruları
Analitik düzlemde x (apsis) ekseninde bütün noktaların y si (ordinatı) sıfır olduğundan x ekseni aynı zamanda y = 0 doğrusudur. y (ordinat) ekseni de x = 0 doğrusudur.
b. x eksenine paralel doğrular
y = k doğrusu; y eksenini k noktasında keser, x eksenine paralel ve y eksenine diktir.
c. y eksenine paralel doğrular
x = k doğrusu; x eksenini k noktasında keser, y eksenine paralel ve x eksenine diktir.
Eksenleri Kestiği Noktaları Bilinen Doğruların Denklemi
x eksenini a noktasında y eksenini de b noktasında kesen doğrunun denklemi
Doğru (a, 0) ve (0, b) noktalarından geçtiğine göre, doğrunun denklemi iki noktadan geçen doğru denklemi özelliği kullanılarak da yazılabilir.
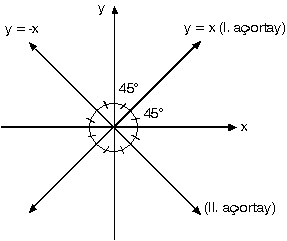
Dik koordinat sisteminde apsisleri ordinatlarına eşit olan noktaların oluşturduğu doğruya
y=x
doğrusu denir.
Dik koordinat sisteminde apsisleri ile ordinatları birbirinin ters işaretlisi olan noktaların oluşturduğu doğruya
y= -x doğrusu denir.
y = x ve y = –x doğruları aynı zamanda koordinat eksenlerinin açıortaylarıdır. Koordinat eksenleri ile yaptıkları açılar 45° dir.
Doğruların Grafikleri
Doğruların grafiklerini çizmek için x ve y eksenlerini kestikleri noktalar bulunur.
x eksenini kestiği nokta için y = 0 ve y eksenini kestiği nokta için x = 0 değerleri alınır.
Noktanın Analitik İncelemesi
Analitik Düzlem:
Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da adlandırılır.
Dik koordinat sistemi
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir. Eksenlerin kesiştiği noktaya orijin denir.
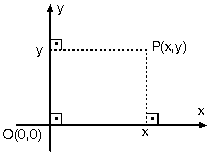
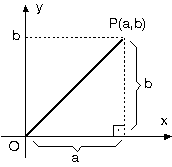
P(x, y) noktası için, x noktanın apsisi, y de ordinatıdır. Apsis ve ordinat değerleri eksenlere çizilen dik doğruların eksenleri kestiği noktalardır.
Orijinin koordinatları O(0,0) dır.
x ekseni üzerindeki noktaların ordinatı sıfırdır. A(a, o) noktası gibi. y ekseni üzerindeki noktaların ise apsisi sıfırdır. B(o, b) noktası gibi.
- Koordinat eksenleri analitik düzlemi dört bölgeye ayırırlar.
I. Bölge: x > 0 y > 0
II. Bölge: x < 0 y > 0
III. Bölge: x < 0 y < 0
IV. Bölge: x > 0 y < 0
İki nokta arasındaki uzaklık
a. Apsisleri veya ordinatları eşit olan noktalar arasındaki uzaklık.
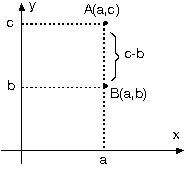
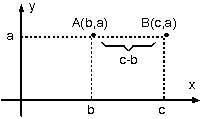
A(b, a) ve B(c, a) noktaları için
|AB| = |c – b|
b. Apsisleri ve ordinatları farklı noktalar arasındaki uzaklık
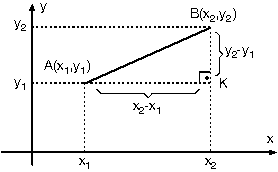
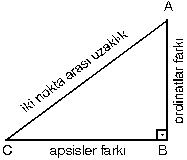
Analitik düzlemde A(x1,y1) ve B(x2,y2) noktaları arasındaki uzaklık |AB| biçiminde gösterilir. A ve B noktalarının analitik düzlemdeki yerleri belirtildiğinde AKB dik üçgeni meydana gelir.
AKB dik üçgeninde [AB] hipotenüsdür. [AK] dik kenar uzunluğu iki noktanın apsisleri farkı (x2 – x1) ve [BK] dik kenar uzunluğu iki noktanın ordinatları farkı (y2 – y1) dir.
Pisagor teoreminden iki nokta arası uzaklık;
eşitliği ile bulunabilir.
Burada x1 ile x2 nin ve y1 ile y2 nin yer değiştirmesi sonucu değiştirmez.
- İki nokta arası uzaklık bulunurken dik üçgenden de yararlanılabilir.
Orta Nokta Koordinatları
Yukarıdaki şekilde A(x1, y1) noktası ile B(x2, y2) noktası veriliyor. [AB] doğru parçasının ortasındaki nokta K(x0, y0) noktası ise
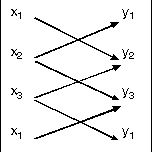
- Köşegenleri birbirini ortalayan dörtgenlerde (kare, dikdörtgen, paralelkenar, eşkenar dörtgen) karşılıklı köşelerin koordinatları toplamları eşittir.
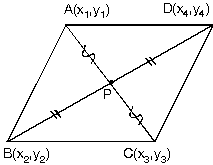
y1 + y3 = y2 + y4
Belli Oranda Bölen Nokta Koordinatları
Belli oranda bölen noktayı bulurken; verilen oranlar ile apsisler farkı ve ordinatlar farkı arasında benzerlikten kaynaklanan bir eşitlik oluşur.
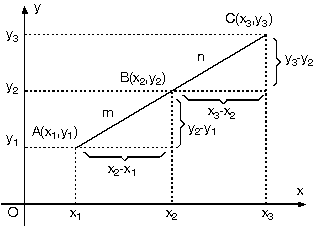
A(x1,y1) , B(x2,y2) ve C(x3,y3) noktaları için,
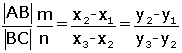
Belli oranda bölen noktayı bulurken yukarıdaki eşitlikten faydalanarak aşağıdaki metod kullanılabilir.
m uzunluğunda (x2 – x1) kadar değişirse
n uzunluğunda (x3 – x2) kadar değişir.
Değişme miktarı artma yada azalma olabilir. Önemli olan noktaların aynı doğrultuda olması ve aynı yönde hareket etmektir. Aynı şeyler ordinatlar için de geçerlidir.
m uzunluğunda (y2 – y1) kadar değişirse
n uzunluğunda (y3 – y2) kadar değişir.
Üçgenin Ağırlık Merkezinin Koordinatları
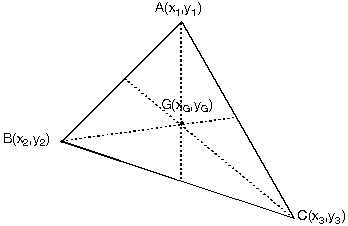
ABC üçgeninin köşe koordinatları
A(x1,y1), B(x2,y2), C(x3,y3) ve ağırlık merkezi G(xG,yG) ise ağırlık merkezi koordinatları:
Bu eşitlikler belli oranda bölen nokta özellikleri kullanılarak elde edilebilir.
Köşe Noktalarının Koordinatları Bilinen Üçgenin Alanı
Köşe koordinatları A(x1,y1), B(x2,y2), ve C(x3,y3) olan ABC üçgeni veriliyor.
Köşe koordinatları bilinen üçgenin alanını bulmak için yukarıda olduğu gibi köşe koordinatları alt alta yazılır. İlk yazılan en alta ilave edilir ve şekildeki gibi çarpılır. Elde edilen sonuç ikiye bölünerek alan değeri bulunur. Alan negatif olamayacağından, sonuç negatifte çıksa pozitif kabul edilir. (Mutlak değeri alınır.)
Üç köşesinin koordinatları bilinen bir üçgenin alanı, üçgen analitik düzlemde çizilerek de bulunabilir.
- Köşe koordinatlarından herhangi ikisinin apsisleri yada ordinatları eşit ise üçgenin kenarlarından biri eksenlere paralel olur. Bu durumda üçgenin alanı çizilerek de bulunabilir.
- Bir üçgenin alanının sıfır çıkması, köşe koordinatları olarak verilen üç noktanın doğrusal üç nokta olduğunu gösterir.