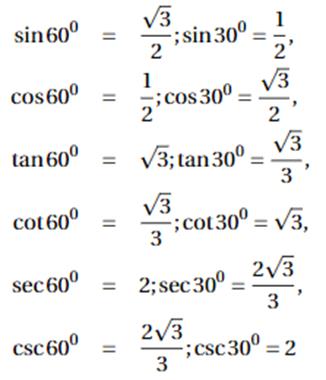Dik Üçgende Trigonometrik Bağıntılar Konu Anlatımı: Sinüs, kosinüs, tanjant gibi trigonometrik oranların dik üçgenlerde nasıl kullanıldığını keşfedin.
Pisagor Teoremi
Pisagor Teoremine göre; bir dik üçgende dik kenarların karelerinin toplamlarının hipotenüsün karesine eşittir.
Pisagor’dan bu yana Pisagor teoremi üzerinde çalışan matematikçiler şöyle bir genellemeye ulaşmıştır:
n pozitif bir doğal sayı olmak üzere;
- a = 2n + 1
- b = 2n2 + 2n
- c = 2n2 + 2n + 1
eşitliklerini sağlayan tüm a, b ve c doğal sayıları, a2 + b2 = c2 eşitliğini de sağlar.
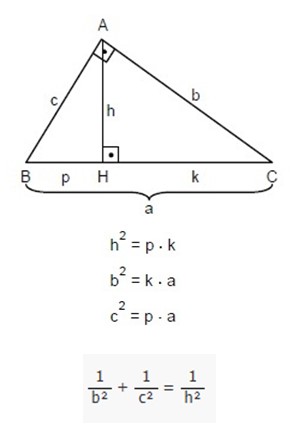
Oklid Teoremi
Bir dik üçgenin dik açının olduğu köşeden karşı kenara indirilen dikme için
DİK ÜÇGENDEKİ ORANLAR
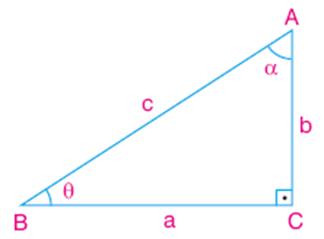
Dik üçgende 90 derece dışındaki diğer açılardan birini seçelim. Örneğin resimde A açısı seçilmiştir. Trigonometrik oranları yazarken resimdeki gibi bir isimlendirme kullanacağız. 90 derecenin karşısındaki kenara hipotenüs, seçtiğimiz açının karşısındaki kenara karşı kenar, geriye kalan ve açının bir kolu olan kenara ise komşu kenar diyeceğiz. İsimlendirme işinde de anlaştığımıza göre gelelim bu kenarları oranlamaya.
BCA dik üçgeninde, aşağıdaki eşitlikleri yazabiliriz.
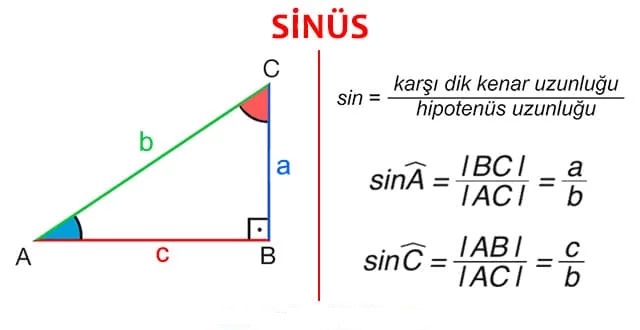
SİNÜS
Bir dik üçgende, bir dar açının karşısındaki dik kenar uzunluğunun hipotenüsün uzunluğuna oranına o dar açının sinüsü denir. Bir A açısının sinüsü “sin A” şeklinde gösterilir.
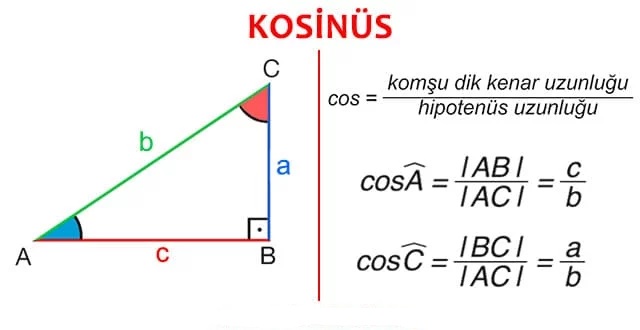
KOSİNÜS
Bir dik üçgende, bir dar açının komşu dik kenar uzunluğunun hipotenüsün uzunluğuna oranına o dar açının kosinüsü denir. Bir A açısının kosinüsü “cos A” şeklinde gösterilir.
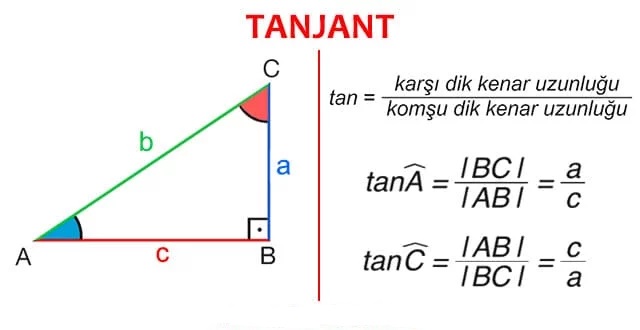
TANJANT
Bir dik üçgende, bir dar açının karşısındaki dik kenar uzunluğunun komşu dik kenar uzunluğuna oranına o dar açının tanjantı denir. Bir A açısının tanjantı “tan A” şeklinde gösterilir.
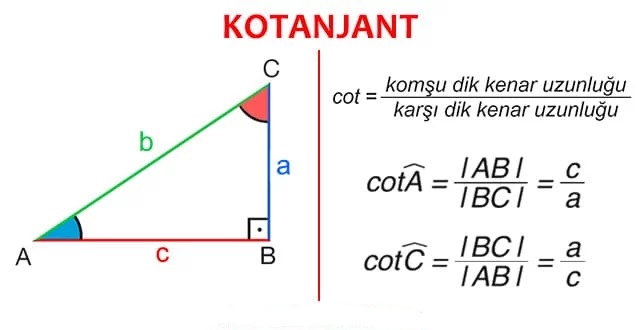
KOTANJANT
Bir dik üçgende, bir dar açının komşu dik kenar uzunluğunun karşısındaki dik kenar uzunluğuna oranına o dar açının kotanjantı denir. Bir A açısının kontanjantı “cot A” şeklinde gösterilir.
Sonuçlar: Ölçüleri toplamı 90° olan (tümler) iki açıdan birinin sinüsü, diğerinin kosinüsüne; birinin tanjantı, diğerinin kotanjantına; birinin sekantı, diğerinin kosekantına eşittir. Buna göre,
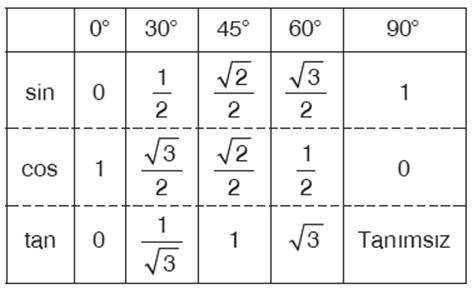
Bazı dar açıların trigonometrik değerleri aşağıda verilmiştir. Bu değerlerin çok iyi bilinmesi soruları daha hızlı çözmenizi sağlar.
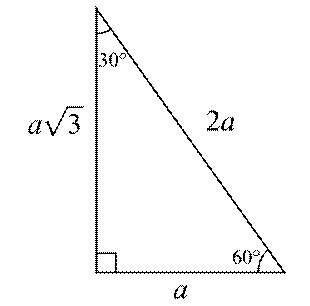
30-60-90 Üçgeni
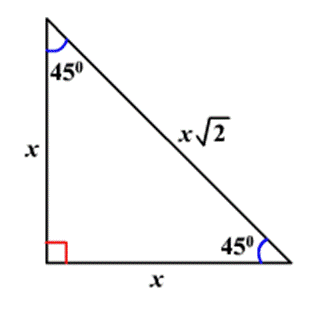
45-45-90 Üçgeni
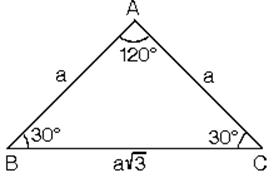
30-120-30 Üçgeni
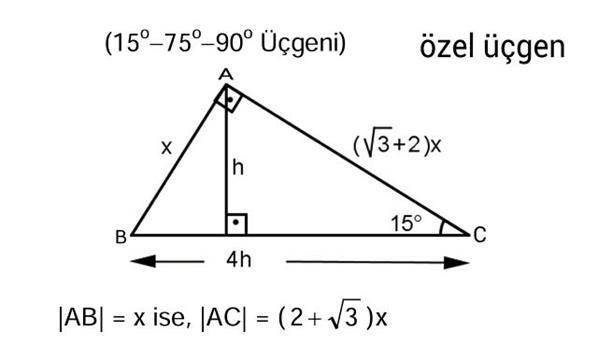
15-75-90 Üçgeni
Örnek1.
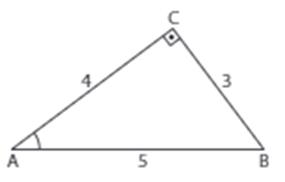
Aşağıdaki ABC dik üçgeninde
|AB| = 5 cm
|AC| = 4 cm
|BC| = 3 cm olarak veriliyor.
Buna göre, A açısının trigonometrik oranlarını bulalım.
Çözüm:
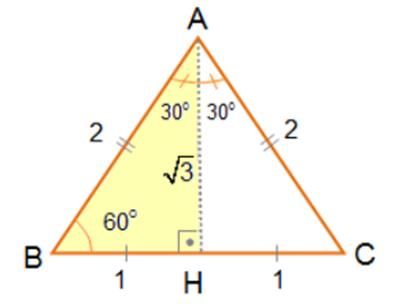
Örnek2. Bir kenar uzunluğu 2 birim olan eşkenar üçgen yardımıyla 300 ve 600 lik açıların trigonometrik fonksiyonlarının değerini bulalım: