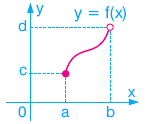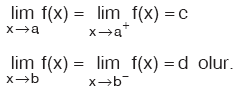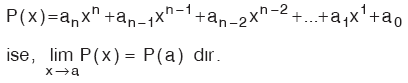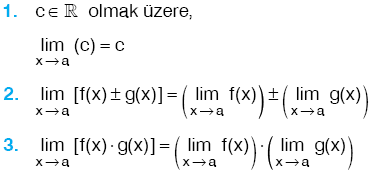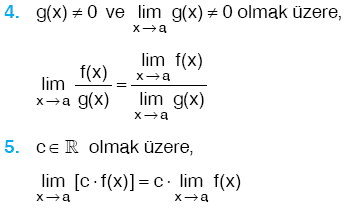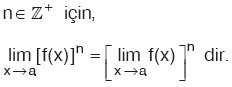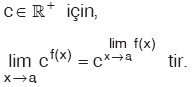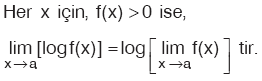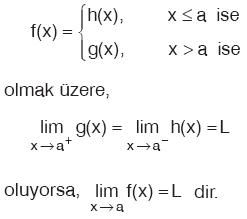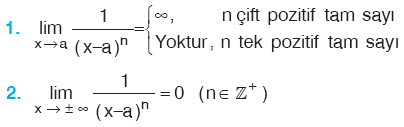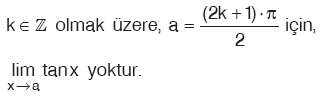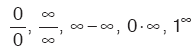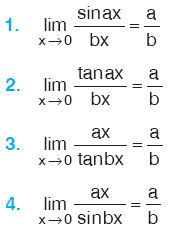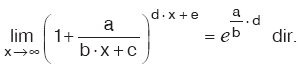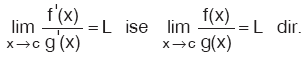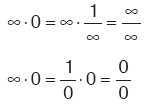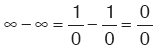Limit ve Süreklilik Konu Anlatımı

Limit ve Süreklilik Konu Anlatımı: Limit kavramının temellerini, fonksiyonların sürekliliğini ve bu konuların analitik matematikteki önemini detaylıca öğrenin.

Limit

Bir f(x) fonksiyonunda x değişkenine bir a değerine sınırsız yaklaşan değerler verildiğinde fonksiyondaki f(x) değerleri de bir L değerine sınırsız yaklaşıyorsa; bu L değerine f(x) fonksiyonunun a değeri için limiti denir. Limit şu şekilde gösterilir:

SOLDAN YAKLAŞMA, SAĞDAN YAKLAŞMA

x değişkeni a ya, a dan küçük değerlerle yaklaşıyorsa, bu tür yaklaşmaya soldan yaklaşma denir ve

biçiminde gösterilir.

x değişkeni a ya, a dan büyük değerlerle yaklaşıyorsa, bu tür yaklaşmaya sağdan yaklaşma denir ve

biçiminde gösterilir.

LİMİT KAVRAMI

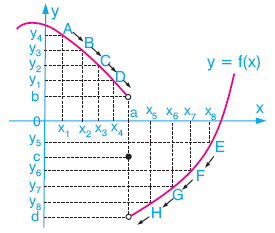
Limit kavramını bir fonksiyonun grafiği üzerinde açıklayalım:

Grafiği verilen y = f(x) fonksiyonu için, apsisleri; x = a nın solunda yer alan ve giderek a ya yaklaşan A(x1, y4) , B(x2, y3) , C(x3, y2) , D(x4, y1), … noktalarını göz önüne alalım:

Bu noktaların apsisleri olan x1, x2, x3, x4, … giderek a ya yaklaşırken, ordinatları f(x1) = y4, f(x2) = y3, f(x3) = y2, f(x4) = y1, … giderek b ye yaklaşır.

Bu durumu; x, a ya soldan yaklaşıyorken f(x) b ye yaklaşır şeklinde ifade edebiliriz. Bu durumda, f(x) in x = a daki soldan limiti b dir denir. Ve

şeklinde gösterilir.

Yukarıdakine benzer şekilde, apsisleri x = a nın sağında yer alan ve giderek a ya yaklaşan E(x8, y5) , F(x7, y6) , G(x6, y7) , H(x5, y8) , … noktalarını göz önüne alalım.

Bu noktaların apsisleri olan x8, x7 , x6 , x5 , … giderek a ya yaklaşırken, ordinatlar f(x8) = y5 , f(x7) = y6 , f(x6) = y7 , f(x5) = y8 , … giderek d ye yaklaşır.

Bu durumu “x, a ya sağdan yaklaşıyorken f(x) d ye yaklaşır.” şeklinde ifade edebiliriz. Bu durumda; f(x) in x = a daki sağdan limiti d dir denir. Ve

biçiminde gösterilir.

Kural:

f(x) fonksiyonunun x = a daki soldan limiti sağdan limitine eşit ise fonksiyonun x = a da limiti vardır ve x in a noktasındaki limiti L ise,

biçiminde gösterilir. x = a daki sağ limit ve sol limit değeri, fonksiyonun x = a daki limitidir. f(x) fonksiyonunun x = a daki soldan limiti sağdan limitine eşit değil ise fonksiyonun x = a da limiti yoktur.

UÇ NOKTALARDAKİ LİMİT

f fonksiyonu [a, b) aralığından [c, d) aralığına tanımlı olduğu için, uç noktalardaki limitleri araştırılırken, sadece tanımlı olduğu tarafın limitine bakılarak sonuca gidilir. Fonksiyonun bir noktada limitinin olması için, o noktada tanımlı olması zorunlu değildir. Buna göre,

Kural:

LİMİTLE İLGİLİ ÖZELLİKLER

Özellik:

f ve g , x = a da limitleri olan iki fonksiyon olsun.

Özellik:

PARÇALI FONKSİYONUN LİMİTİ

Özellik:

İŞARET FONKSİYONUNUN LİMİTİ

Özellik:

f(x) = sgn [g(x)] olsun.

Bu sonuç genellikle doğrudur. Fakat az da olsa bu sonuca uymayan örnekler vardır. Söz gelimi, f(x) = sgn[(x²)] fonksiyonunun x = 0 da limiti vardır ve 1 dir.

TAM DEĞER FONKSİYONUNUN LİMİTİ

Özellik:

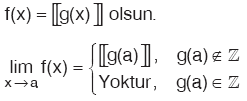
Bu sonuç genellikle doğrudur. Fakat az da olsa bu sonuca uymayan örnekler vardır. Söz gelimi, f(x)=[(x²)] fonksiyonunun x = 0 da limiti vardır.

NİN x = a DAKİ LİMİTİ

Özellik:

TRİGONOMETRİK FONKSİYONLARIN LİMİTİ

sinx in ve cosx in limiti

sinx ve cosx fonksiyonu bütün x reel değerleri için tanımlı olduğu için,

olur.

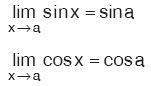
tanx in limiti

tanx fonksiyonu k∈ Z olmak üzere,

koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,

olur.

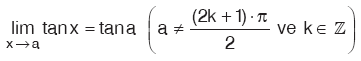
Sonuç

cotx in limiti

cotx fonksiyonu k∈ Z olmak üzere, x≠kπ koşuluna uyan bütün x reel değerleri için tanımlı olduğu için,

olur.

Sonuç

BELİRSİZLİK DURUMLARI

belirsizlikleriyle karşılaştığımızda aşağıda verilen yöntemler kullanılarak limit hesaplanır. Bu limitler türevin içinde vereceğimiz L’Hospital kuralıyla da hesaplanabilir.

Kural

Kural:

m, n Î N olmak üzere,

olur.

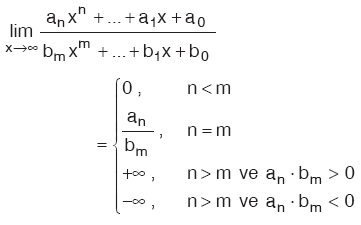
Kural:

a > 0 olmak üzere, ¥ – ¥ belirsizliği olan limitler,

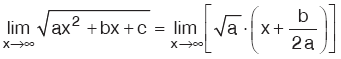
kuralını kullanarak hesaplanabilir.

Kural:

Buna göre, 0 × ¥ belirsizliği

veya belirsizliğine dönüştürülerek sonuca gidilir.

Kural:

SÜREKLİLİK

Kural:

f(x) fonksiyonu apsisi x = a olan noktada süreklidir.

Sonuç:

y = f(x) fonksiyonu x = a da sürekli ise,

Uyarı:

f(x) fonksiyonu apsisi x = a olan noktada sürekli değil ise, süreksizdir.

Kural:

Bir fonksiyon bir noktada tanımsız ise, o noktada süreksizdir.
Bir fonksiyon bir noktada limitsiz ise, o noktada süreksizdir.
Bir fonksiyon bir noktada tanımlı ve limitli ancak, tanım değeri limit değerinden farklı ise, bu noktada süreksizdir.

L’HOSPİTAL KURALI

Bir fonksiyonun x = a noktasındaki limiti hesaplanırken karşımıza çıkan,

belirsizlikleri,

belirsizliklerinden birine dönüştürülerek, L’ Hospital Kuralı yardımıyla sonuçlandırılır.

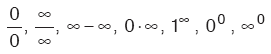
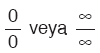
Kural

f ve g, (a, b) aralığında türevlenebilir olsun. Her x ∈ (a, b) için g’(x) ¹ 0 ve c ∈ (a, b) olmak üzere,

Eğer, 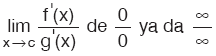ise yukarıdaki kural bir daha uygulanır.

Uyarı

L’ Hospital kuralında 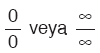belirsizliğini ortadan kaldırmak için, yapılan işlemin: Payın türevini paya, paydanın türevini paydaya yazmak olduğuna dikkat ediniz.

Kural

Sonusz × 0 belirsizliğinde,