Modern Atom Teorisi Konu Anlatımı

Modern Atom Teorisi Konu Anlatımı

BOHR ATOM MODELİ
1913 yılında Niels Bohr, atomları çekirdek etrafında dairesel yörüngelerde hızla dönen elektronlarla çevrili tanecikler olarak tasarladı. İlk bakışta Güneş’in etrafında dönen gezegenleri andıran bu model kolay benimsendi. Bu sistemde atom çekirdeği Güneş, elektronlar ise gezegen olarak düşünüldüğünde zıt yüklerin çekimi merkezkaç kuvveti ile dengelenmekte idi.

Not: Bohr atom modeli, 1H, 2He⁺ ve 3Li²⁺ gibi tek elektrona sahip taneciklerin spektrumlarını açıklar. Bu sistemde bu elektronun belirli yörüngelerde bulunabileceğini söylemiştir.

Bohr atom modeli her yörüngenin belirli bir enerjisi ol- duğundan hareket eden elektronların da belirli bir ener- jisinin olmasını yani kuantlaşması gerektiğini söyler. Bohr; uyarılmış bir hidrojen atomunun ışıma yapmasını, uyarılmış hidrojen atomundaki elektronun daha düşük enerjideki bir yörüngeye düşmesiyle elde edilen fotonun (kuantum enerjisi) yayılmasıyla açıklamıştır.

Bohr, tek elektronlu sistemlere ait enerji hesabında atom numarası ve yörünge numarasını içeren bir eşitlik üretmiştir. Elde edilen bu eşitlik incelendiğinde elekt- ronlar her bir üst yörüngeden temel seviyeye geçerken farklı enerjileri olan fotonlar yaydığı görülür.

Bohr atom modeli çok elektronlu atom ve iyonların emisyon (yayılma) spektrumlarını açıklamada yetersiz kalmış ve dairesel yörünge kavramını açıklayamamıştır. Elektronların küçük tanecikler gibi ikili yapıda davran- ması (tanecik ve dalga) sebebiyle taneciğin hızı ve yeri aynı anda belirlenememiştir. Bu Heisenberg belirsizlik

İlkesi e¢x·¢v >h/4rm o denklemi ile ifade edilir. Bu çalışmalar sonucunda elektronların dairesel bir yörüngede değil belli bir olasılık dâhilinde olan bir bulut bölgesinde olabileceği sonucuna ulaşılmıştır.

Özetleyecek olursak Bohr Atom Teorisi’ne göre,

• Elektronlar çekirdeğin etrafında dairesel yörüngelerde hareket eder.
• Yörüngelerin belirli bir enerjisi vardır. Bu yörüngeler rakamlarla (1, 2, 3, 4, …) ya da harfler (K, L, M, N, …) ile gösterilebilir.
• Bu atomların 1 ya da K enerji düzeyi temel hâl enerji düzeyidir. (Tek elektronlu tanecik olduklarından.)
• Atomlar dışarıdan enerji aldıklarında uyarılmış hâle geçer ve aldığı enerjiyi tekrar geri verip temel hâle dönerken ışın (Emisyon yapar.)

Bohr Atom Modelinin Sınırlılıkları

Bohr atom modeli sadece tek elektronlu tanecikler için geçerlidir. Çok elektronlu atomlarda yörüngelerde bulu- nan orbitallerin enerjileri farklı olduğundan bu modelin uygulanması mümkün değildir. Bohr atom modelinde bahsedilen dairesel yörünge ifadesi, elektronların yeri ve hızı aynı anda belirlenemeyeceğinden yetersiz kalmıştır.

MODERN ATOM TEORİSİ

Atomun Kuantum Modeli (Kuantum Mekaniği)

Atomun kuantum modeli bir atomdaki elektronun tam yerinin belirlenememesine rağmen, elektronun belirli bir zaman diliminde yoğun olarak bulunabileceği bölgeleri açıklamaktadır. Bu fonksiyon ile elektron yoğunluğu yani olasılığı belli eden elektron bulutu ifadesi meydana gelir.

Atomun kuantum modeline göre elektronlar bulunma olasılıklarının yüksek olduğu yerlerde hareket eder. Elektronların bulunma olasılığının yüksek olduğu matematiksel fonksiyonlarla ifade edilen bölgelere orbital denir. Bu fonksiyonlarda bulunan ve elektronların bulunma olasılığının belirlemesine katkı sağlayan sayılara kuantum sayıları denir.

Bohr atom modelinde geçen yörünge kavramı ile, atomun kuantum modelinde bahsedilen orbital kavramları arasındaki karşılaştırma şu şekilde ifade edilebilir:

Yörünge ve Orbital (Elektron Bulutu) Karşılaştırması

Yörünge	Orbital (Elektron Bulutu)
Elektronların dairesel bir yolda ilerlediği varsayılır.	Elektronların yeri kesin belli değildir, bulunma olasılığın yüksek olduğu bölgeler var- sayılır.
Elektronlar düzlemsel hare- ket eder.	Elektronlar üç boyutlu hare- ket eder.
Her yörüngenin belli bir enerji düzeyi vardır.	Her orbitalin belli bir enerji düzeyi vardır.
Her yörüngenin elektron alma kapasitesi vardır.	Bir orbital en fazla iki elekt- ron alabilir.

Kuantum Sayıları

Kuantum sayıları, orbitallerin ve bu orbitallerde yer alan elektronların belirlenmesinde kullanılır. Kuantum mekaniğinde elektronların dağılımlarını açıklamak için üç kuantum sayısı gereklidir.

Bu kuantum sayıları aşağıda verilmiştir.

• Baş kuantum sayısı n
• Açısal momentum kuantum sayısı ¬
• Manyetik kuantum sayısı m¬

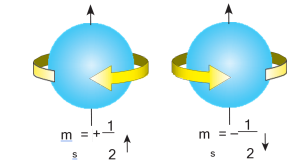
Spin kuantum sayısı ms diye bilinen dördüncü kuantum sayısı ise belirli bir elektronun dönme yönünü belirleyen bir sayıdır.

Baş (Birincil) Kuantum Sayısı (n)

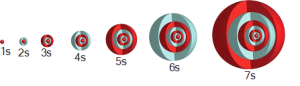
Baş kuantum sayısı (n) 1, 2, 3, 4, … gibi tam sayılar ile ifade edilir. Bu sayılar hidrojen atomunun enerji düzeylerini belirlerken çok elektronlu atomlarda, belirli bir orbitaldeki elektronun çekirdeğe olan ortalama uzaklığını verir. Baş kuantum sayılarına kabuk adı da verilebilir. Baş kuantum sayısı arttıkça elektronun çekirdeğe olan ortalama uzaklığı ve bulunabilecek orbital ve elektron sayıları da artar.

Açısal Momentum (İkincil, Yan) Kuantum Sayısı (¬)

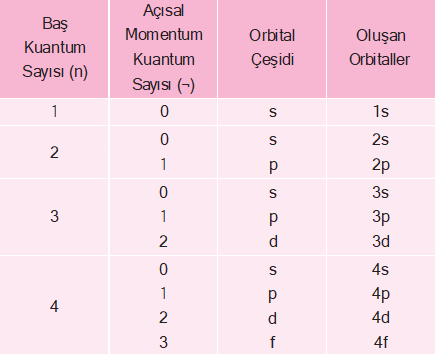
Açısal momentum kuantum sayısı (¬) orbitallerin türlerini ve şekillerini belirler. Açısal momentum kuantum sayı- sının alacağı değerler (orbital türleri) baş kuantum sayı- sına bağlıdır. Herhangi bir n değeri için ¬’nin alabileceği değerler, 0 ile n – 1 arasındaki tam sayılardır.

• n = 1 için; ¬ = 0
• n = 2 için; ¬ = 0 ve 1
• n = 3 için; ¬ = 0, 1 ve 2
• n = 4 için ¬ = 0, 1, 2 ve 3

Açısal momentum kuantum sayısı, baş kuantum sevi- yelerinin de alt enerji seviyelerine ayrıldığını gösterir. Bu sayıların karşılığı olan orbital türleri vardır. Bu seviyele- re karşılık gelen orbital türleri çizelgedeki gibidir.

¬	0	1	2	3
Orbital Türü	s	p	d	f

Buna göre ¬ = 0 olduğunda s orbitali, ¬ = 1 olduğunda p orbitali, ¬ = 2 olduğunda d orbitali ve ¬ = 3 olduğunda f orbitali anlamına gelir. Baş kuantum sayısı ve açısal momentum kuantum sayıları ile aşağıdaki orbitaller bulunur.

Bu orbitallerden s orbitalleri küreseldir.

Merkezinde çekirdeğin bulunduğu bir küredir.

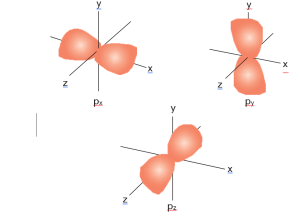
İkinci kabuktan itibaren bulunan p orbitali ise x, y ve z eksenleri boyunca uzanan fiyonk şeklindedir. Yönlenmelerinden dolayı px, py ve pz olarak üç orbital oluşturur.

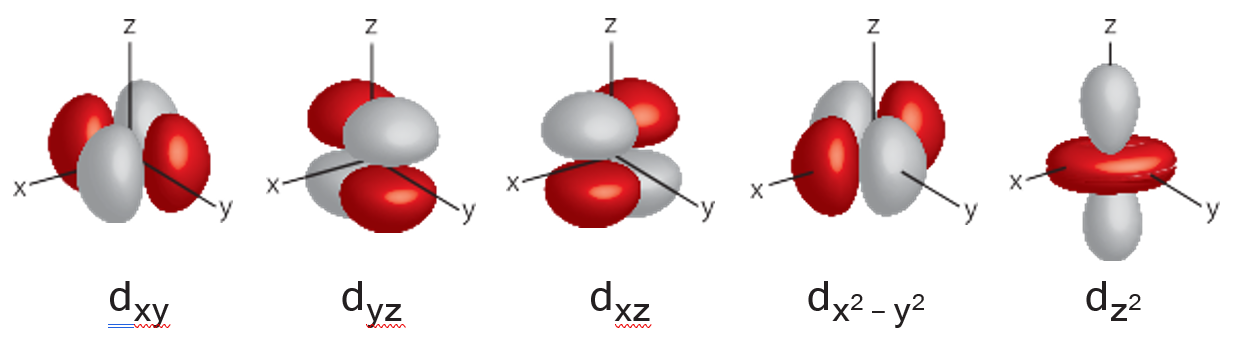
Üçüncü kabuktan itibaren bulunan d orbitali farklı şekil- lerde   bulunur.   Bu   orbitaller orbitaller   dxz,   dxy,   dyz,   dx2 – y2 ve dz2 olarak adlandırılır.

Dördüncü kabuktan itibaren ortaya çıkan f orbitali eş enerjili yedi orbitale sahiptir. Başkuantum sayısı aynı olan orbitallerde enerji sırala- ması s < p < d < f şeklindedir.

Manyetik Kuantum Sayısı (m¬)

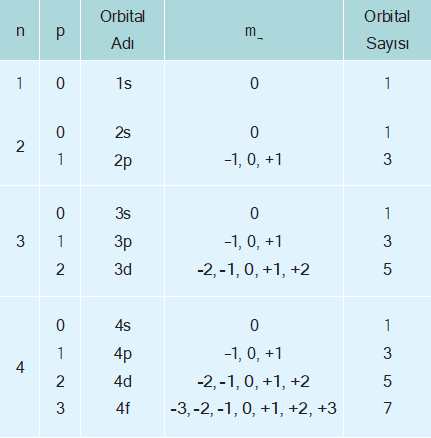
Orbitallerin uzayda yönlenmelerini gösteren bir sayı- dır. Bir alt kabuk için m¬ nin alabileceği değerler açısal momentum kuantum sayısına bağlıdır. Herhangi bir ¬ değerine karşılık aşağıda verildiği gibi (2¬ +1) adet m¬ değerleri bulunabilir.

m¬ = –¬ … 0, … + ¬ değerlerini alabilir.

¬ = 0 ise m¬ = 0

¬ = 1 ise m¬ = –1, 0 , +1

¬ = 2 ise m¬ = –2, –1, 0 , +1, +2

¬ = 3 ise m¬ = –3, –2, –1, 0, +1, +2, +3 olur.

Her bir baş kuantum sayısının altında n² kadar orbital bulunur. Bir ¬ alt kabuğundaki orbital sayısı m¬ sayısı kadardır, bu da 2¬ + 1 kadardır.

Spin Kuantum Sayısı (mS)

Elektronun kendi ekseni etrafında dönmesine spin denir. Bir orbitaldeki elektronun saat yönü ve tersi olarak iki yönde dönme hareketi yaptığı varsayılır.

Elektron Dağılımı

Bir atomun elektron dağılımında baş kuantum sayısı ve diğer kuantum sayıları dikkate alınarak elektronların nasıl yerleştirildiği gösterilir.

Not: Elektron sayısı ve dizilişi aynı olan taneciklere izoelektronik tanecikler denir. Elektron dizilimi yapmadan izoelektronikliği belirlemek zordur. Elektron dağılımına bakılarak atomun bazı özellikleri hakkında tahminler yürütülebilir. Nötr bir atomun elektron dizilimi atomun fiziksel ve kimyasal özellikleri hakkında fikir edinmemizi sağlar.

Aufbau Kuralı

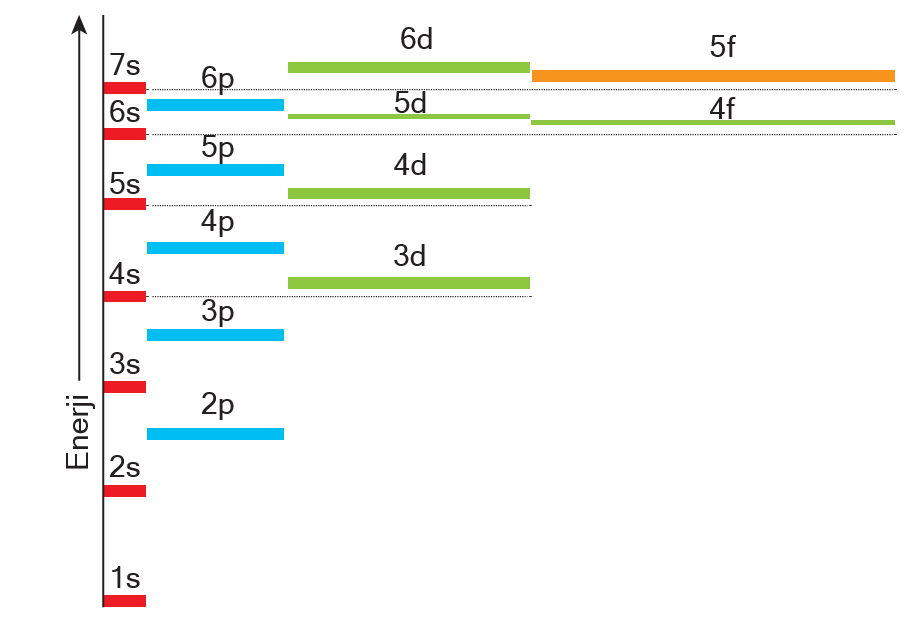
Aufbau” kelimesi Almancada inşa ya da bina etmek anlamına gelmektedir. Nasıl bir bina alt kattan başlana- rak inşa ediliyorsa atomdaki elektronlar da düşük ener- jili orbitaller doldukça yüksek enerjili orbitallere geçecek şekilde doldurulur. Orbitallerin enerji sıralaması elekt- ron diziliminde çok önemlidir. Enerji sıralamasını ezbere bilmek zor olabilir. Orbitallerin enerjinin sıralaması aşa- ğıdaki şekildeki gibidir.

Bu listedeki orbitallerin enerjilerini ezberlemek yerine Kletchkowski-Madelung İlkesi’ne göre orbital enerjile- ri karşılaştırılabilir. Bu kurala göre orbitallerin enerjisi (n + ¬) değerinin artmasıyla artar. (n + ¬) değeri eşit olan- larda n değeri büyük olanın orbital enerjisi daha büyük olur. Bu kurala göre orbital enerji sıralaması küçükten büyüğe doğru aşağıdaki gibidir.

1s < 2s < 2p < 3s < 3p < 4s < 3d < 4p < 5s < 4d < 5p < 6s < 4f < 5d …

(n + ¬) değerleri 1 2 3 3 4 4 5 5 5 6 6 6 7 7

Aşağıda bazı element atomlarına ait elektron dizilimleri verilmiştir.

2He: 1s² 3Li: 1s²2s¹

5B: 1s²2s²2p¹

6C: 1s²2s²2p²

7N: 1s²2s²2p³

9F: 1s²2s²2p⁵

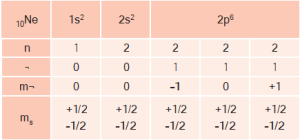
10Ne: 1s²2s²2p⁶

Pauli İlkesi

Bu ilkeye göre bir atomda dört kuantum sayısı aynı olan iki elektron bulunamaz. Bir orbital en fazla 2 elektron alabilir. Elektronlar aynı orbitalde bile olsalar zıt spinli şekilde yerleşmeleri gerekir.

Hund Kuralı

Elektronlar eş enerjili orbitallere yerleşirken öncelikle her orbitale bir elektron eş spinli olacak şekilde yerleşir. Bütün eş enerjili orbitaller yarı dolu hâle geldikten sonra diğer elektronlar zıt spinli olarak orbitallere yerleşir.

Küresel Simetri

Bir atomun elektron dizilimindeki son orbitallerin her birinin tam ya da yarı dolu hâlde bulunmasına kü- resel simetri denir. Küresel simetri atoma kararlı- lık kazandırdığından küresel simetrik elektron da- ğılımına sahip atomdan elektron koparmak küresel simetrik olmayanlara göre daha zordur. Elektron dizilimi (s¹, p³, d⁵, f⁷) ile biterse   yarı   dolu   kararlılık, (s², p⁶, d¹⁰, f¹⁴) ile biterse tam dolu kararlılık hâlini alır. Bu kararlılığın sebebi elektronların orbitallere homojen olarak dağılmasından dolayı elektronların çekirdek ta- rafından eşit kuvvette çekilmesidir.

Aşağıda bazı atomlara ait elektron dizilimleri ve orbital gösterimleri verilmiştir.

3Li    : 1s²2s¹                         Küresel simetri görülür.

2He : 1s²                              Küresel simetri görülür.

11Na : 1s²2s²2p⁶3s¹             Küresel simetri görülür.

10Ne : 1s²2s²2p⁶                  Küresel simetri görülür.

O    : 1s²2s²2p⁴                   Küresel simetri görülmez.

9F     : 1s 2s 2p                   Küresel simetri görülmez.

14Si : 1s²2s²2p⁶3s²3p²           Küresel simetri görülmez.

6C : 1s²2s²2p²      Küresel simetri görülmez.

Bazı durumlarda enerjileri birbirine yakın orbitallerdeki elektronlar yer değiştirerek atomun daha kararlı bir yapıya ulaşmasını sağlar. Bu durumdaki elementlerden ikisi 24Cr ve 29Cu’dur. Bu atomların elektron dizilimleri yapıldığında; 24Cr: 1s²2s²2p⁶3s²3p⁶4s²3d⁴ ortaya çıkar. Ancak gerçek dizilimde 4s orbitalindeki 1 elektron 3d orbitaline yerleşmiştir.

Bu durumda atom daha kararlı elektron dizilimi olan 24Cr: 1s²2s²2p⁶3s²3p⁶4s¹3d⁵ hâlini tercih eder. 29Cu: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d⁹ ortaya çıkar. Ancak gerçek dizilimde, 4s orbitalindeki 1 elektron 3d orbitaline yerleşmiştir. Bu durumda atom daha kararlı elektron dizilimi olan 29Cu: 1s²2s²2p⁶3s²3p⁶4s¹3d¹⁰ hâlini tercih eder.

İyonların Elektron Dizilimi Anyonların Elektron Dizilimi

Negatif yüklü taneciklerin (anyon) elektron dizilimi ya- pılırken şu yol izlenir: Taneciğin nötr hâlindeki elekt- ron sayısına aldığı yük kadar elektron eklenir. Toplam elektron sayısı üzerinden elektron dizilimi yapılır.

8O: 1s² 2s² 2p⁴   iken 😯^2-: 1s² 2s² 2p⁶ olur.

7N: 1s² 2s² 2p³   iken 7N^3-: 1s² 2s² 2p⁶ olur.

17Cl: 1s²2s²2p⁶3s²3p⁵ iken 17Cl^–: 1s²2s²2p⁶3s²3p⁶ olur.

Katyonların Elektron Dizilimi

Pozitif yüklü taneciklerin (katyon) elektron dizilimi ya- pılırken taneciğin nötr hâlindeki elektron dizilimi ya- zılır. Daha sonra pozitif yük sayısı kadar elektron, bu elektron diziliminden çıkarılarak yeni elektron di- zilimi elde edilir. Bu çıkarma yapılırken ilk olarak baş kuantum sayısı büyük olan orbitalden elektron koparılır.

Baş kuantum sayıları aynı ise önce enerjisi büyük olan orbitalden elektron koparılır.

11Na : 1s² 2s² 2p⁶ 3s¹ iken 11Na⁺: 1s² 2s² 2p⁶ olur.

26Fe²⁺: 1s²2s²2p²3s²3p⁶3d⁶

35Br : 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁵ iken

35Br³⁺ : 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p²

35Br⁵⁺ : 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰

35Br⁷⁺ : 1s² 2s² 2p⁶ 3s² 3p⁶ 3d¹⁰ olur.

Değerlik Orbitali ve Değerlik Elektronları

Bir atomun en yüksek enerjili orbitallerine değerlik orbitali, bu orbitallerde bulunan elektronlara ise değerlik elektronu denir. Değerlik elektronları bir atomun kim- yasal özellikleri hakkında bilgi verir. Değerlik elektronu eşit olan atomlar benzer kimyasal özellik gösterir ve genellikle periyodik cetvelde de aynı grupta bulunur. Değerlik orbitalleri ve değerlik elektron sayısı bulunurken temel hâl elektron diziliminin son terimleri önemlidir. Eğer elektron dizilimi s ile bitiyorsa değerlik orbitali s, değerlik elektron sayısı ise s orbitalindeki elektron sayısıdır.

3Li: 1s²2s¹ (Değerlik orbitali 2s, değerlik elektron sayısı 1’dir.)

12Mg: 1s²2s²2p⁶3s² (Değerlik orbitali 3s, değerlik elekt- ron sayısı 2’dir.)

Eğer elektron dizilimi p ile bitiyorsa değerlik orbitalleri s ve p, değerlik elektron sayısı ise s ve p orbitalindeki elektron sayısıdır.

7N: 1s²2s²2p³ (Değerlik orbitalleri 2s ve 2p, değerlik elektron sayısı 5’tir.)

10Ne: 1s²2s²2p⁶ (Değerlik orbitalleri 2s ve 2p, değerlik elektron sayısı 8’dir.)

35Br: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d¹⁰ 4p⁵ (Değerlik orbital- leri 4s ve 4p değerlik elektron sayısı 7’dir.)

Eğer elektron dizilimi d ile bitiyorsa değerlik orbitalleri s ve d, değerlik elektron sayısı ise s ve d orbitalindeki elektron sayısıdır.

22Ti: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d² (Değerlik orbitalleri 4s ve 3d, değerlik elektron sayısı 4’tür.)

26Fe: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s² 3d⁶ (Değerlik orbitalleri 4s ve 3d, değerlik elektron sayısı 8’dir.)

24Cr: 1s² 2s² 2p⁶ 3s² 3p⁶ 4s¹ 3d⁵ (Değerlik orbitalleri 4s ve 3d, değerlik elektron sayısı 6’dır.)