Temel Kavramlar Konu Anlatımı ile her alanda temel kavramların önemini, nasıl kullanıldıklarını ve neden öğrenmemiz gerektiğini daha iyi anlayın.
Matematik temel kavramlar neler?
TEMEL KAVRAMLAR
A: SAYI
Sayıları ifade etmeye yarayan sembollere rakam denir. Ör: 0,1,2,3,4,5,6 Rakamların çokluk belirtecek şekilde bir araya getirilmesiyle oluşturulan ifadeler ifadesine sayı denir.
| Not: Her rakam bir sayıdır. Fakat bazı sayılar rakam değildir. |
- SAYI KÜMELERİ
- Sayma Sayıları: {1, 2, 3, …, n, …} kümesinin her bir elemanına sayma sayısıdenir.
- Doğal Sayılar: {0, 1, 2, 3, …, n, …} kümesinin her bir elemanına doğal sayıdenir. Şeklinde gösterilir.
- Pozitif Doğal Sayılar= {1, 2, 3, 4, …, n, …} kümesinin her bir elemanına pozitif doğal sayıŞeklinde gösterilir.
| Not: Sayma sayıları kümesindeki her elemana pozitif doğal sayı da denir. |
- Tam Sayılar:{…, – n, … – 3, – 2, – 1, 0, 1, 2, 3, … , n , …} kümesinin her bir elemanına tam sayıdenir. Şeklinde gösterilir.
Tam sayılar kümesi; negatif tam sayılar kümesi: şeklinde, pozitif tam sayılar kümesi: şeklinde gösterilir ve sıfırı eleman kabul eden: {0} kümenin birleşim kümesidir.
Buna göre, dır.
- Rasyonel Sayılar: a ve b birer tam sayı ve b ¹0 olmak koşuluyla biçiminde yazılabilen sayılara rasyonel sayılar denir.
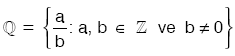
- İrrasyonel Sayılar: Rasyonel olmayan sayılara irrasyonel sayılar denir. Virgülden sonra belli bir kurala göre gitmeyen sayılar irrasyonel sayılardır. İrrasyonel sayılar kümesi şeklinde gösterilir.
Buna göre, kümesinin elemanları şeklinde gösterilemez.
(a, b Î ve b ¹0)
| Not: Rasyonel ve aynı zamanda irrasyonel olan bir sayı yoktur. |
Sayıları irrasyonel sayısına birer örnektir.
- Reel (Gerçel) Sayılar: Rasyonel sayılar kümesiyle irrasyonel sayılar kümesinin birleşimi olan kümeye reel (gerçel) sayılar kümesi denir.
Şeklinde gösterilir.
- Karmaşık (Kompleks) Sayılar:
- SAYI ÇEŞİTLERİ
- Çift Sayı
Olmak üzere (yani tam sayı) 2n genel ifadesi ile belirtilen tam sayılara çift sayı denir.
Ç = {…, –2n, …, –4, –2, 0, 2, 4, …, 2n , …} kümesinin elemanlarının her biri çift sayıdır.
- Tek Sayı
olmak üzere 2n + 1 ifadesi ile belirtilen tam sayılara tek sayı denir.
T = {…, – (2n + 1), …, –3, –1, 1, 3, …, (2n + 1), …} kümesinin elemanlarının her biri tek sayıdır.
İki tek sayının farkı çift, toplama çift ve çarpımı tek sayıdır
K bir tek sayı olmak üzere,
- K + K sonucu çift sayıdır.
- K – K sonucu çift sayıdır.
- K ×K işleminin soncu tek sayıdır.
İki çift sayının toplamı, farkı ve çarpımı çift sayıdır.
Ç bir çift sayı olmak üzere,
- Ç + Ç işleminin sonucu çift
- Ç – Ç işleminin sonucu çift
- Ç ×Ç işleminin sonucu çift sayıdır.
Bir tek sayı ile bir çift sayının toplamı ve farkı tek sayı çarpımı çift sayıdır.
T bir tek sayı ve Ç bir çift sayı olmak üzere,
- T + Ç işleminin sonucu tek,
- Ç + T işleminin sonucu tek,
- T – Ç işleminin sonucu tek,
- Ç – T işleminin sonucu tek,
- T ×Ç işleminin sonucu çift sayıdır.
| Not 1: Tam sayılar kümesinde bir çarpma işleminin sonucunda sonuç çift ise, çarpma işlemine giren sayılardan en az biri çifttir. Not 2: Tam sayılar kümesinde bir çarpma işleminin sonucunda sonuç tek ise, çarpma işlemine giren sayıların her biri tek sayıdır. Not 3: Çift sayıların tüm pozitif tam kuvvetleri yine bir çift sayıdır. Çünkü Not:1 deki kural geçerli olur. Buna göre, n pozitif tam sayı ve Ç bir çift sayı olmak üzere, Çn nin sonucu daima çift sayıdır. Not 3: Tek sayıların tüm doğal sayı kuvvetleri yine bir tek sayıdır. Çünkü Not 2’deki kural geçerli olmaktadır. Buna göre, n bir doğal sayı ve T bir tek sayı olmak üzere, Tn nin sonucu daima tek sayıdır Not 4: Bölme işlemi için yukarıdaki şekilde bir genelleme yapmak yanlış olacaktır. |
| Not:
· Tek sayılar ve çift sayılar tam sayılardan oluşur. · Hem tek aynı zamanda da çift olan bir sayı yoktur. · Sıfır (0) çift sayıdır. |
- Pozitif Sayılar – Negatif Sayılar
Sıfırdan büyük her reel (gerçel) sayılara pozitif sayı, sıfırdan küçük her reel (gerçel) sayılara negatif sayıdenir.
a < b < 0 < c < d olmak üzere,
- a ve b negatif sayı
- c ve d pozitif sayıdır.
- İki pozitif sayının toplamı pozitiftir. (c + d > 0)
- İki negatif sayının toplamı negatiftir. (a + b < 0)
- Çıkarma işleminde eksilen çıkandan büyük ise sonuç (fark) pozitif, eksilen çıkandan küçük ise fark negatif olur.
- Zıt işaretli iki sayıyı toplamak için; işaretine bakılmaksızın büyük sayıdan küçük sayı çıkarılır ve büyük sayının işareti sonuca verilir.
- Aynı işaretli iki sayının çarpımı (ya da bölümü) pozitiftir.
- Zıt işaretli iki sayının toplamı; negatif, pozitif veya sıfırdır.
- Zıt işaretli iki sayının çarpımı (ya da bölümü) negatiftir.
- Pozitif sayının bütün kuvvetleri pozitiftir.
- Negatif sayının tek kuvvetleri negatif, çift kuvvetleri pozitiftir.
- Asal Sayı
Kendisinden ve 1’den başka pozitif tam sayılara tam bölünmeyen 1 den büyük doğal sayılara asal sayıdenir.
2, 3, 5, 7, 11, 13, 17, 19 sayıları birer asal sayıdır.
- En küçük asal sayı 2 dir. 2’den başka çift asal sayı yoktur.
- Asal sayıların çarpımı asal değildir.
| Not: Asal olmayan, 1’den büyük tam sayılara bileşik sayı denir. |
- Aralarında Asal
Ortak bölenlerinin en büyüğü 1 olan tam sayılara aralarında asal sayılardenir.
a ile b aralarında asal ise, aralarındaki oran en sade biçimdedir.
- ARDIŞIK SAYILAR
Belirli bir kurala göre art arda gelen sayı dizilerine ardışık sayılar denir.
n bir tam sayı olmak üzere,
- Ardışık dört tam sayı sırasıyla;
n, n + 1, n + 2, n + 3 tür.
- Ardışık dört çift sayı sırasıyla;
2n, 2n + 2, 2n + 4, 2n + 6 dır.
- Ardışık dört tek sayı sırasıyla;
2n + 1, 2n + 3, 2n + 5, 2n + 7 dir.
- Üçün katı olan ardışık dört tam sayı sırasıyla;
3n, 3n + 3, 3n + 6, 3n + 9 dur.
Bazı Ardışık Sayıların Toplamı
n bir sayma sayısı olmak üzere,
- Ardışık sayma sayılarının toplamı
Şeklinde formül ortaya çıkar.
- Ardışık pozitif çift doğal sayıların toplamı ise
2 + 4 + 6 + … + (2n) = n (n + 1)
- Ardışık tek doğal sayıların toplamı
1 + 3 + 5 + … + (2n – 1) = n2
- Artış miktarı eşit olan ardışık tam sayıların toplamı
Terim sayısı
Terim Sayı= [(Son Terim – İlk Terim) / Artış Miktarı] + 1
r: İlk terim
n: Son terim
x: Artış miktarı olmak üzere,
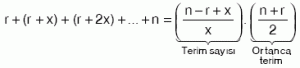
| Not: Artış miktarı eşit olan ardışık sayıların toplamı, sayı adedine bölünürse ortanca terim bulunur. Eğer sayı adedi çift ise, ortanca terim sayı dizisine ait değildir. |







