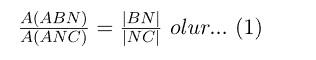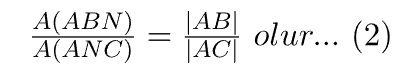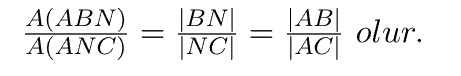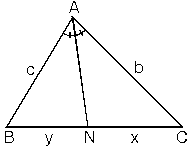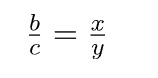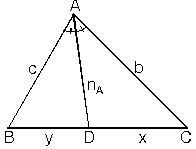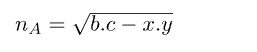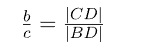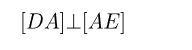Üçgende Açıortay Bağıntıları Konu Anlatımı: Üçgenlerde açıortayların özelliklerini, oluşturdukları geometrik ilişkileri ve çeşitli problemlerdeki uygulamalarını öğrenin.
ÜÇGENDE AÇIORTAY
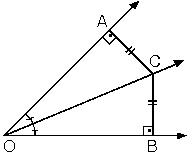
Herhangi bir açının ölçüsünü iki eş açıya bölen ışınlara açıortay denir. Şekilde AOB açısını iki eş açıya ayıran [OC ışınına açıortay denir.
Açıortay üzerindeki herhangi bir noktadan açının kenarlarına çizilen dik uzunluklar eşittir.
AOB bir açı,
[OC açıortay
m(AOC) = m(COB)
|AC| = |CB|
AOC ve BOC eş üçgenler olduğundan |OA| = |OB|
İç Açıortay Bağıntısı
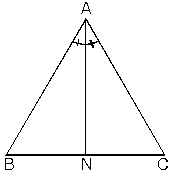
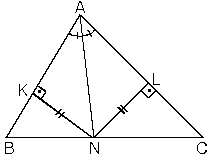
ABC üçgeninde [AN] açıortay ABN ve ANC üçgenlerinin[BC] tabanına göre, yükseklikleri eşit olduğundan
ABN üçgeninde [AB] kenarına ait yükseklik ANC üçgeninde[AC] kenarına ait yüksekliğe eşittir.
[AN] açıortay olmak şartıyla bu iki alan oranını birleştirirsek; (1) ve (2) den
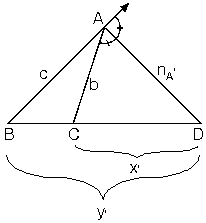
ABC üçgeninde [AN] açıortay olmak şartıyla
İç Açıortay Uzunluğu
ABC üçgeninde A köşesinden çizdiğimiz açıortay uzunluğuna nA dersek
Dış Açıortay Bağıntısı
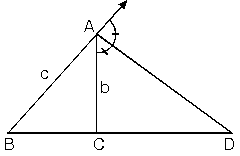
ABC üçgeninde [AD], A köşesine ait dış açıortaydır.
Dış Açıortay Uzunluğu
ABC üçgeninde [AD] dış açıortayının uzunluğuna n’A dersek
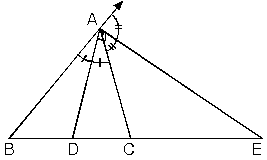
İç açıortayla dış açıortay arasındaki açı
m(DAE)=90°
ABC üçgeninde [AD] iç açıortayı ile [AE] dış açıortayı arasındaki açı için
2a + 2b = 180°
a + b = 90° dir.
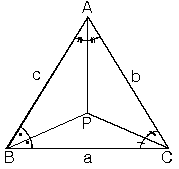
Bir üçgende iç açıortayların kesim noktası iç teğet çemberin merkezidir.
P noktasının kenarlara uzaklığı eşittir. Merkezden indirilen dikmeler iç teğet çemberin yarıçapı olur.