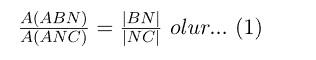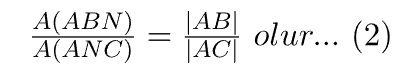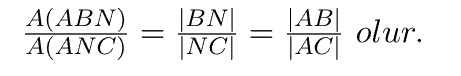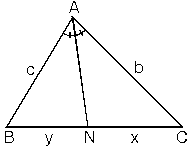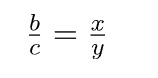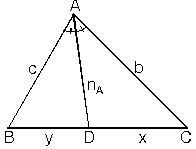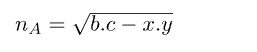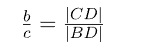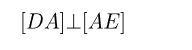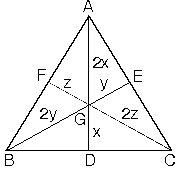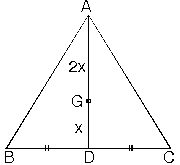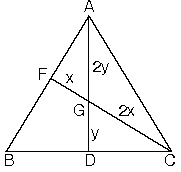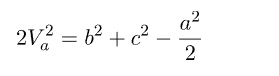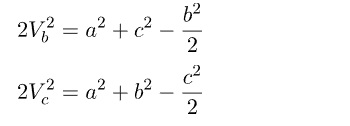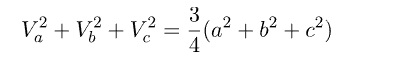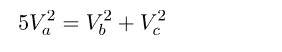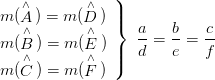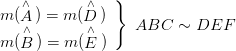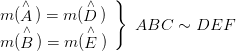Üçgende Açıortay, Kenarortay ve Benzerlik Konu Anlatımı ile geometrinin temel yapı taşlarını keşfedin. Bu kavramların derinlemesine analizleri ve uygulamaları!
ÜÇGENDE AÇIORTAY
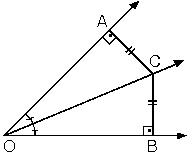
Herhangi bir açının ölçüsünü iki eş açıya bölen ışınlara açıortay denir. Şekilde AOB açısını iki eş açıya ayıran [OC ışınına açıortay denir.
Açıortay üzerindeki herhangi bir noktadan açının kenarlarına çizilen dik uzunluklar eşittir.
AOB bir açı,
[OC açıortay
m(AOC) = m(COB)
|AC| = |CB|
AOC ve BOC eş üçgenler olduğundan |OA| = |OB|
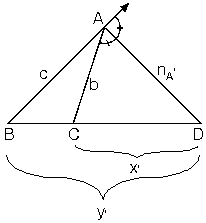
İç Açıortay Bağıntısı
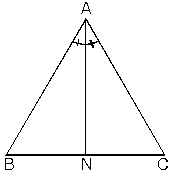
ABC üçgeninde [AN] açıortay ABN ve ANC üçgenlerinin[BC] tabanına göre, yükseklikleri eşit olduğundan
ABN üçgeninde [AB] kenarına ait yükseklik ANC üçgeninde[AC] kenarına ait yüksekliğe eşittir.
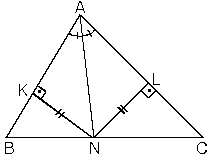
[AN] açıortay olmak şartıyla bu iki alan oranını birleştirirsek; (1) ve (2) den
ABC üçgeninde [AN] açıortay olmak şartıyla
İç Açıortay Uzunluğu
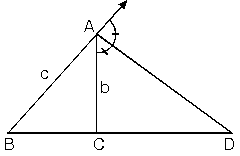
ABC üçgeninde A köşesinden çizdiğimiz açıortay uzunluğuna nA dersek
Dış Açıortay Bağıntısı
ABC üçgeninde [AD], A köşesine ait dış açıortaydır.
Dış Açıortay Uzunluğu
ABC üçgeninde [AD] dış açıortayının uzunluğuna n’A dersek
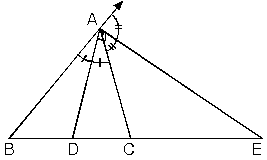
İç açıortayla dış açıortay arasındaki açı
m(DAE)=90°
ABC üçgeninde [AD] iç açıortayı ile [AE] dış açıortayı arasındaki açı için
2a + 2b = 180°
a + b = 90° dir.
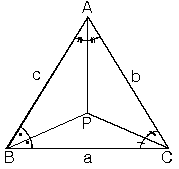
Bir üçgende iç açıortayların kesim noktası iç teğet çemberin merkezidir.
P noktasının kenarlara uzaklığı eşittir. Merkezden indirilen dikmeler iç teğet çemberin yarıçapı olur.
ÜÇGENDE KENARORTAY
Ağırlık Merkezi
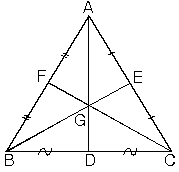
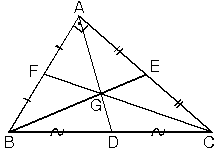
Üçgenlerde kenarortaylar bir noktada kesişirler. Kenarortayların kesişim noktasına ağırlık merkezi denir.
Ağırlık merkezi kenarortayı, kenara 1 birim, köşeye 2 birim olacak şekilde böler.
Bir üçgende iki kenarortayın kesişmesiyle oluşan nokta ağırlık merkezidir.
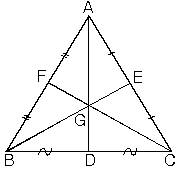
ABC üçgeninde [AD] kenarortay ve |AG| = 2|GD| olduğundan G noktası ağırlık merkezidir.
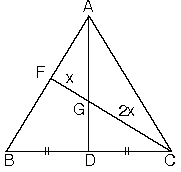
ABC üçgeninde [AD] kenarortay ve |CG| = 2|FG|olduğundan G noktası ağırlık merkezidir.
ABC üçgeninde |AG| = 2|GD| ve |CG| = 2|GF| eşitliğini sağlayan G noktası ABC üçgeninin ağırlık merkezidir.
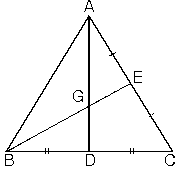
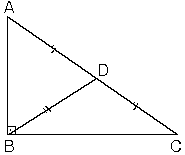
Dik üçgende hipotenüse ait kenarortay hipotenüsün yarısına eşittir.
ABC dik üçgeninde [BD] hipotenüse ait kenarortay ve |AG|=|DC|=|BD|
Kenarortayların Böldüğü Alanlar
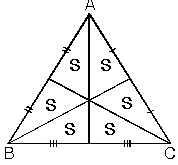
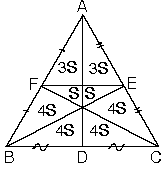
Kenarortaylar üçgenin alanını altı eşit parçaya bölerler.
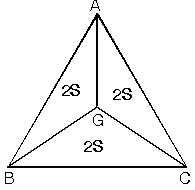
G ağırlık merkezi köşelere birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.
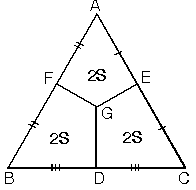
G ağırlık merkezi kenarların orta noktaları ile birleştirildiğinde üçgenin alanı üç eşit parçaya bölünür.
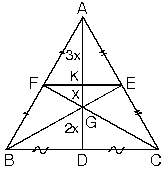
ABC üçgeninde kenarortaylar ve [FE] çizilirse
|AK| = 3x ; |KG| = x ; |GD| = 2x eşitlikleri bulunur.
K noktası [AD] kenarortayının orta noktasıdır.
[FE] //[BC] ve 2[FE]=[BC]
ABC üçgeninde kenarortaylar ve [FE] çizildiğinde şekildeki gibi bir alan bölünmesi oluşur.
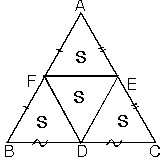
Kenarların orta noktalarını birbirine birleştirdiğimizde üçgenin alanı dört eşit parçaya bölünür.
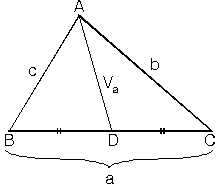
Kenarortay Uzunluğu
ABC üçgeninde A köşesinden çizilen kenarortayın uzunluğuna Va dersek
Bu bağıntı diğer kenarortaylar içinde geçerlidir.
Kenarortaylar taraf tarafa toplanırsa
Dik Üçgende Kenarortaylar
A açısı 90° olan bir dik üçgende kenarortaylar arasında
ÜÇGENDE BENZERLİK
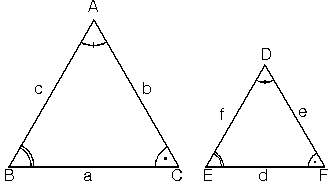
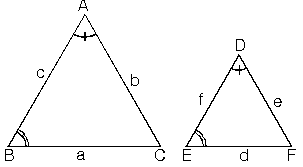
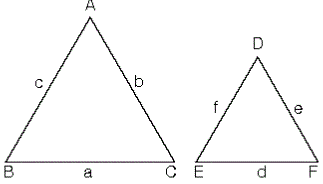
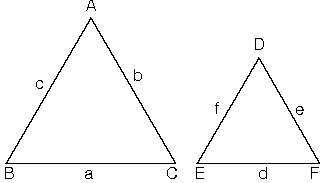
Karşılıklı açıları eş ve karşılıklı kenarları orantılı olan üçgenlere benzer üçgenler denir.
ABC ve DEF üçgenleri için;
Buradan ABC üçgeni ile DEF üçgeni benzerdir denir ve ABC ~ DEF biçiminde gösterilir.
eşitliğinde verilen k sayısına, benzerlik oranı yada benzerlik katsayısı denir.
k = 1 olan benzer üçgenlerde karşılıklı kenarlar eşit olduğundan, bu üçgenlere eş üçgenler denir.
ABC ~ DEF benzerliği yazılırken eş açıların sıralanmasına dikkat edilir.
Açı – Açı Benzerlik Teoremi
Karşılıklı ikişer açıları eş olan üçgenler benzerdir.
şekilde verilen üçgenlerde
İkişer açıları eş olduğundan, üçüncü açıları da eş olmak zorundadır. Dolayısıyla bu iki üçgen benzer üçgenlerdir.
m(C)=m(F)
Kenar – Açı – Kenar Benzerlik Teoremi
İki üçgenin karşılıklı ikişer kenarı orantılı ve bu kenarların oluşturduğu karşılıklı açılar eş ise, üçgenler benzerdir.
ABC üçgeni ile DEF üçgeninin BAC ve EDF açıları eş, bu açıların kenarları da orantılı ise, bu iki üçgen benzerdir.
BAC açısının kısa kenarının EDF açısının kısa kenarına oranı, BAC açısının uzun kenarının EDF açısının uzun kenarına oranına eşittir.
Kenar – Kenar – Kenar Benzerlik Teoremi
İki üçgenin karşılıklı bütün kenarları orantılı ise bu iki üçgen benzerdir.
şekilde verilen üçgenlerde
Kenarları orantılı olan ABC ve DEF benzer üçgenlerinde orantılı kenarları gören açılar eştir.
m(A) = m(D),
m(B) = m(E),
m(C) = m(F)
Temel Benzerlik Teoremi
ABC üçgeninde [DE] // [BC] ise yöndeş açılar eş olacağından ADE ~ ABC dir.
Buradan da
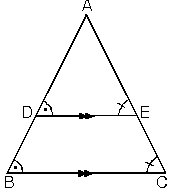
Ağırlık merkezinden çizilen paralel doğru kenarları 1 birime 2 birim oranında böler. ABC üçgeninde G ağırlık merkezi ve [KL] // [BC]
|AK|=2|KB|, |AL|=2|LC|
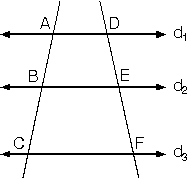
Tales Teoremi
Paralel doğrular kendilerini kesen doğruları aynı oranda bölerler. d1 // d2 // d3 doğruları için
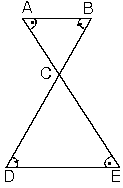
[AB] // [DE] ise oluşan içters açıların eşitliğinden, ABC ~ EDC olur. Buradan,
eşitliği elde edilir. Buna kelebek benzerliği de denir.
Benzerlik Özellikleri
Benzer üçgenlerin açıları karşılıklı olarak eş, diğer bütün elemanları orantılıdır.
ABC ~ DEF ise
Burada k ya benzerlik oranı denir.
Benzer üçgenlerde orantılı kenarlara ait yüksekliklerin oranı benzerlik oranına eşittir.
Benzer üçgenlerde orantılı kenarlara ait kenar-ortay uzunluklarının oranı benzerlik oranına eşittir.
Benzer üçgenlerde eş açılara ait açıortay uzunluklarının oranı benzerlik oranına eşittir.
Benzer üçgenlerin çevrelerinin oranı benzerlik oranına eşittir.
ABC üçgeninde içteğet çemberin yarıçapı ve çevrel çemberin yarıçapı , DEF üçgeninde içteğet çemberin yarıçapı ve çevrel çemberin yarıçapı olsun.