Üçgende Alanlar Konu Anlatımı: Üçgenlerin alan hesaplamalarını öğrenin; farklı tiplerdeki üçgenler için alan formüllerini ve uygulama yöntemlerini keşfedin.
Üçgenin Alanı
Üçgende alan geometrinin en önemli konularından biridir. Çünkü alan hesabı geometrinin diğer konularında da vardır ve üçgenin alanı bunun başlangıcıdır. Bir üçgenin alanı herhangi bir kenara ait yükseklikle o kenarın uzunluğunun çarpımının yarısına eşittir.
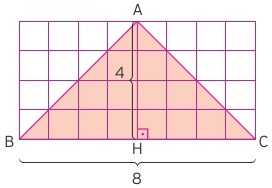
Şekildeki ABC üçgeninde alan |BC|.|AH|/2 şeklinde olur. |BC| kenarı 8 birim, yüksekliği olan |AH| kenarı da 4 birim olduğu için alan 8.4/2 = 16 birim2 bulunur. Şekildeki dörtgenin alanı için de iki kenarı çarpmamız yeterli olacaktı. Bunu dörtgenler konusunda daha iyi göreceğiz. Ancak üçgenin içinde bulunduğu dörtgenin alanın yarısı olması neden 2 ye böldüğümüzü göstermesi açısından önemlidir.
Dikkat ederseniz her kare kenarına 1 birim uzunluk verilmiştir. Üçgenin alanı taralı alanlardan oluşmaktadır. Bütün dikdörtgenin alanını sayarsanız 32 kare üçgen içindeki taralı alanları sayarsanız da 16 kare bulursunuz. Bu da formülümüzün görsel ispatı olmaktadır.
Üçgende alan hesaplarken hangi kenarı seçtiğinizin önemi yoktur. Önemli olan seçtiğiniz kenar ile o kenara ait yüksekliği çarpmanızdır. Bu yükseklik üçgen içinde olabileceği gibi üçgen dışında da olabilmektedir.
Üçgensel Bölgenin Alanı
Bir düzlemde var olan herhangi bir üçgensel bölgenin alanını hesaplarken farklı yöntemlerle alan hesabı yapabiliriz. Örneğin bir üçgeni iki farklı üçgensel bölgeye ayırıp alanları toplamını bulmamız da üçgenin alanını bulmamız için yeterlidir.
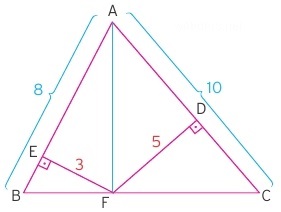
Yukarıdaki üçgende |AF| doğru parçasını çizersek üçgeni iki üçgensel bölgeye ayırırız. Bu durumda iki küçük üçgende kenarlara ait yükseklikler belli olduğu için alan hesabı daha kolay olacaktır. Sonuçta üçgenin alanı: 8.3/2 + 10.5/2 = 37 olacaktır.
Dik Üçgende Alan
Dik üçgen için alan hesabı yapmak çok kolaydır. Zaten bir kenar ve o kenara ait yükseklik üçgen içerisinde mevcuttur. Dik kenarların çarpımının yarısı bize dik üçgenin alanını verir. Bununla birlikte bir örnek yapalım. Örneği çözerken de dik üçgenle ilgili bildiklerimizi hatırlayalım.
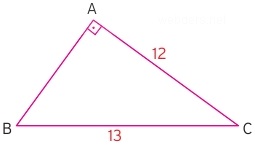
Soru: Dik ABC üçgeninde |AC| = 12 cm, |BC| = 13 cm uzunluğundadır. Buna göre bu üçgenin alanını bulunuz.
Çözüm: Bir dik üçgenin alanını bulmak için iki dik kenarın uzunluğuna ihtiyacımız vardır. Ancak bu örnekte bir dik kenar uzunluğu ile birlikte hipotenüs uzunluğu verilmiştir. Eksik dik kenarın uzunluğunu Pisagor bağıntısı yardımıyla elde ederiz. Burada hesaplamaya bile gerek duymadan 5-12-13 özel üçgeni olduğu bilgisini kullanırız. Bu durumda |AB| kenarının uzunluğunun 5 cm olduğunu elde ederiz.
Çözümün ikinci adımı ise yine çok kolaydır. Dik kenarlardan birinin uzunluğu 5 cm, diğerinin 12 cm ise alan = 5.12/2 = 30 cm2 olur.
Üçgenin alanı sadece alan hesaplamak için kullanılmaz. Bazen uzunluk bilgisini de alan bilgisini kullanarak elde edebiliriz. Şimdi de bununla ilgili bir örnek yapalım.
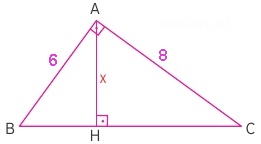
Yukarıdaki üçgende iki kenar uzunluğu 6 cm ve 8 cm olarak verilmiştir. Buna göre hipotenüse indirilen dikme uzunluğu x ne kadardır?
Çözüm: Burada üçgenin alanının her iki taraftan da aynı çıkacağı bilgisini kullanmalıyız. Soruyu 4 adımda çözebiliriz.
- Üçgenin alanı 6.8/2 = 24 olur.
- Pisagor bağıntısından 6-8-10 üçgeni ile |BC| kenarı 10 cm bulunur.
- x/2 = 24 eşitliği alandan dolayı kurulur.
- x = 4,8 cm bulunur.
Geniş Açılı Üçgenin Alanı
Geniş alanı üçgende de alan aynı şekilde hesaplanır. Ancak bu üçgende yüksekliği görmek temel düzeyde geometri yeteneği gerektirebilir. Çünkü yükseklik çoğunlukla üçgenin dışında yer almaktadır. Geniş açıyı oluşturan kenarlara ait yükseklikler dışarıdan çizilmektedir.
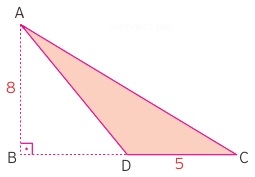
Yukarıdaki üçgende alan 8.5/2 = 20 olur. Yüksekliğin içerden veya dışarıdan olmasının bir önemi yoktur.
Üçgende alan sorularında her zaman üçgenin alanı sorulmaz. Bazen alan verilip kenar uzunlukları da sorulabilir. Burada yapılması gereken sadece denklemin tersten kurulmasıdır.
Özel Üçgenlerin Alanı
Özel üçgenler işlem yapabileceğim açı ölçülerine veya kenar eşitliklerine sahip üçgenlerdir. Bu üçgenlerde alan hesaplamak için üçgenlere ait özellikleri kullanıp veri elde ederiz.
Eşkenar Üçgenin Alanı
Eşkenar üçgende bütün kenarlar eşit olduğu için sadece bir kenarın uzunluğunu bilmek bize alanı hesaplama konusunda yeterli olacaktır. Bunun için formülü bilmemiz yeterlidir. Ancak formülü vermeden önce bu formülün nerden geldiğini ispatlamalıyız. Eşkenar üçgen konusunda bir kenarı a birim olan üçgenin yüksekliğinden söz etmiştik.
- Kenar uzunluğu: a birim.
- Yükseklik uzunluğu: a√3/2
- Alan = a.(a√3/2)/2 = a2√3/4 elde edilir.
Yukarıda elde edilen formül bütün eşkenar üçgen sorularında alan formülü olarak kullanılabilir. Sadece a yerine üçgenin kenar uzunluğunu koymamız yeterlidir.
Sinüs Alan Formülü
Özel açılı üçgenlerde açıların trigonometrik bağıntılarını biliriz. Bilmesek bile kolaylıkla hesaplayabiliriz. Bu nedenle özel üçgenlerde sinüs alan formülü çok işimize yarar. Bu formül uygulandığında herhangi bir dikliğe ihtiyacımız yoktur.
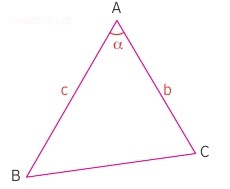
Yukarıdaki üçgende alan için herhangi bir dikmeye ihtiyaç yoktur. Kesişen iki kenarın uzunluğu ile bu kenarlar arasındaki açının sinüsünü çarpıp ikiye bölmemiz bize alanı verecektir. Yani yukarıdaki üçgende b.c.Sinα/2 bize alanı verecektir.
Aslına bakarsanız dikliğin olduğu sorularda da aynı formül geçerlidir. Sadece sin90 = 1 olduğu için çarpımda yazılmaz. Yoksa sinüs genel formül içerisinde mutlaka yer alır.
Özel üçgenlerde çeşitli doğru parçaları çizerek daha düzgün üçgenler elde edebiliriz.
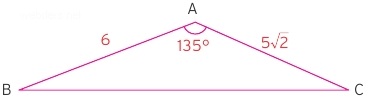
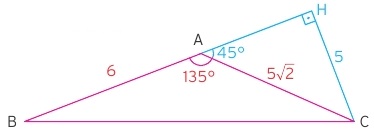
Yukarıdaki soruda 135 derecelik bir açı barındıran üçgen verilmiştir. Bu açı ölçüsü bir üçgeni özel üçgen yapabilmektedir. Alan için kenar ve o kenara ait yüksekliğe ihtiyaç duyduğumuza göre dikme inerek soruyu çözelim.
|AB| kenarı 6 birim, bu kenara ait dışarıdaki yükseklik de 5 birim bulunur. Bu durumda alan 5.6/2 = 15 br2 bulunur.
Aynı soruyu sinüslü alan formülünden de çözebiliriz. Sin135 = Sin45 =√2/2 bilgisini bilmemiz yeterlidir. Bu durumda alan (6.5√2 ).(√2/2)/2 = 15 bulunur yine. Eğer sinüs alan formülüne ve açıların trigonometrik değerlerine hakimseniz bu tür sorularda çizime dahi ihtiyaç duymayabilirsiniz.
Üçgende Alan Oranları
Eğer iki üçgenin yükseklikleri eşitse alanları oranı taban alanlarının oranına eşittir. Çarpımın genel ilkesi gereği bu böyledir. Bu durum genellikle bölünmüş üçgenlerde karşımıza çıkar.
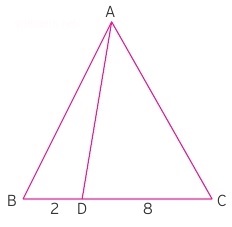
Yukarıdaki üçgende ADC üçgeninin alanı ABD üçgenini alanının 4 katı kadardır. Çünkü 8/2 = 4 eşitliği vardır. Yükseklik aynı olduğu için alanlar arasında taban uzunlukları ile orantılı bir durum vardır. Bu soru 1998 yılında üniversite sınavında çıkmıştır. ABD üçgenin alanı 6 cm2 olduğu verilmiş ve ABC üçgeninin alanı sorulmuştur. Oran mantığı ile ADC üçgeni 24 cm2 olacak ve büyük üçgen de 30 cm2 olacaktır. Soru bu kadar kolaydır.
Üçgenin Alanı ile İlgili Diğer Kurallar
Üçgende kenarortay, açıortay, ağırlık merkezi gibi kavramlar alan konusunda da etkilidirler.
Kenarortay Alan ilişkisi
Kenarortaylar üçgeni alan açısından eş parçalara bölerler. Zaten kenarın ortalanması demek iki eşit alan ortaya çıkması demektir.
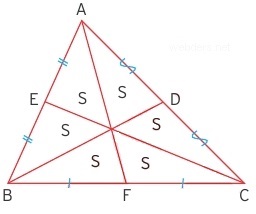
Yukarıdaki üçgende üç kenarortay bir araya gelerek üçgeni 6 eş parçaya ayırmıştır. Üç kenarortay ağırlık merkezinde kesiştiği için ağırlık merkezi de bu konuda ayrıca rol oynar. Aşağıda ağırlık merkezinin üçgeni alan açısından üç parçaya ayrıldığı gösterilmiştir.
Açıortay Alan İlişkisi
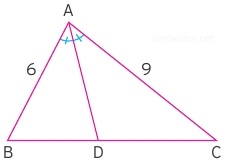
Açıortayda kenar uzunluklarının oranı açıortayın kestiği kenara oranlı bir şekildedir. Dolayısıyla alanlar da bu orandadır. Bir örnek üzerinde bunu daha iyi anlayabiliriz.
Yukarıdaki şekilde ADC 24 cm2 olduğuna göre ABD kaç cm2 olur? Soruda açıortay verildiği için 9/6 = 3/2 dir. Alanlar da kenar uzunluklarına göre 3 e 2 olacak şekilde dağılacaktır. Bu durumda ABD = 16 cm2 olur.