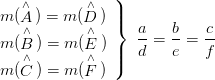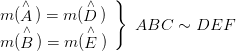Üçgende Eşlik ve Benzerlik Konu Anlatımı: Üçgenler arasındaki eşlik ve benzerlik kurallarını keşfedin; bu kavramların geometrideki önemini ve uygulamalarını öğrenin.
Üçgenlerde Eşlik Nedir?
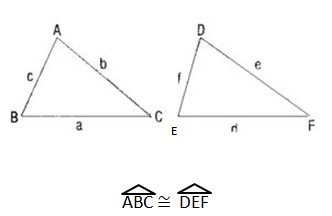
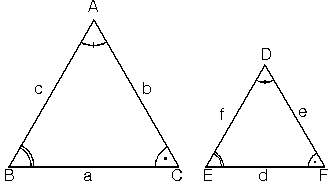
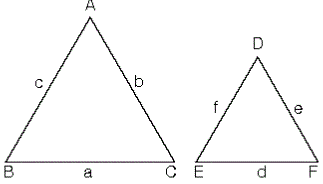
Eğer iki üçgenin karşılıklı kenarlarının boyutları ve iç açılarının ölçüleri aynıysa, bu iki üçgen birbirine eşittir. Bu tür eşitlik durumları, “≅” işareti kullanılarak ifade edilir. Bu sembolle iki üçgenin eşitliğini gösterirken, karşılıklı eş açılar aynı sıra ile belirtilmelidir.
ABC ile DEF üçgenleri arasında yapılan ABC ↔ DEF eşlemesinde karşılıklı kenarlar ve karşılıklı açılar eş ise, bu eşleme bir eşliktir.
Üçgenlerde Eşlik Şartları
Eğer iki üçgenin tüm kenarlarının uzunlukları ve iç açılarının değerleri birbiriyle aynıysa, bu durumda söz konusu üçgenler birbirine eşittir. Ancak, her zaman iki üçgenin tüm kenar ve açıları bilinmeyebilir. Böyle durumlarda, elimizdeki sınırlı bilgilerle iki üçgenin eş olup olmadığını belirleyebiliriz.
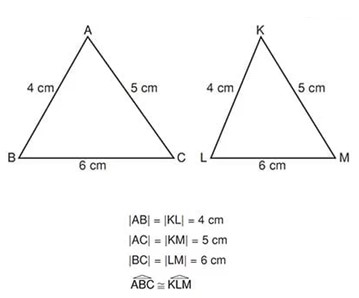
Kenar – Kenar – Kenar Eşlik Şartı (KKK)
İki üçgenin karşılıklı üçer kenarı eş ise, bu iki üçgen eştir.
Kenar – Açı – Kenar Eşlik Şartı (KAK)
İki üçgen arasında birebir eşleme yapıldığında ikişer kenar uzunlukları ve bu iki kenar arasında kalan açılarının ölçüleri eşit ise bu üçgenler eş üçgenlerdir. Buna; Kenar – Açı – Kenar (KAK) eşlik şartı denir.
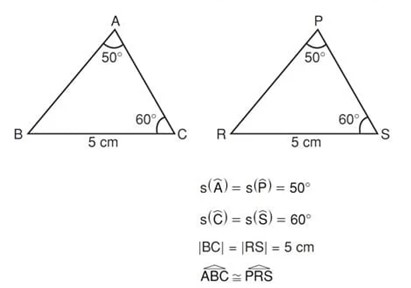
Açı – Kenar – Açı Eşlik Şartı (AKA)
İki üçgenin ikişer açıları ile bu açıların köşelerini birleştiren kenarları karşılıklı olarak eş ise, bu iki üçgen eştir.
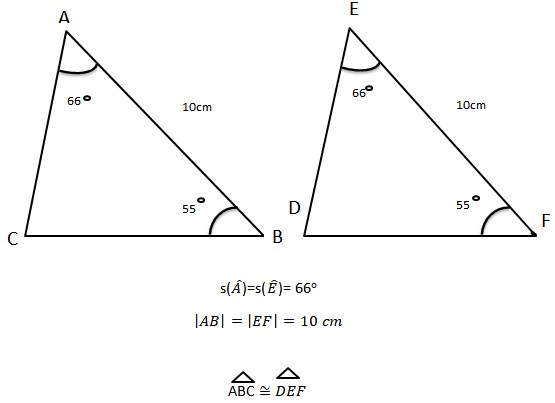
Kenar – Açı – Açı Eşlik Şartı (KAA)
İki üçgen arasında birebir eşleme yapıldığında ikişer açılarının ölçüleri ve bu açılardan herhangi birinin karşısındaki kenarın uzunlukları eşit ise bu üçgenler eş üçgenlerdir. Buna; Kenar – Açı – Açı (KAA) eşlik şartı denir.
ÜÇGENDE BENZERLİK
Karşılıklı açıları eş ve karşılıklı kenarları orantılı olan üçgenlere benzer üçgenler denir.
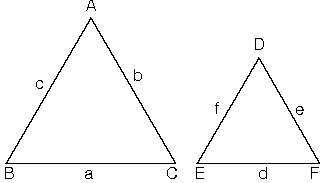
ABC ve DEF üçgenleri için;
Buradan ABC üçgeni ile DEF üçgeni benzerdir denir ve ABC ~ DEF biçiminde gösterilir.
eşitliğinde verilen k sayısına, benzerlik oranı yada benzerlik katsayısı denir.
k = 1 olan benzer üçgenlerde karşılıklı kenarlar eşit olduğundan, bu üçgenlere eş üçgenler denir.
ABC ~ DEF benzerliği yazılırken eş açıların sıralanmasına dikkat edilir.
Açı – Açı Benzerlik Teoremi
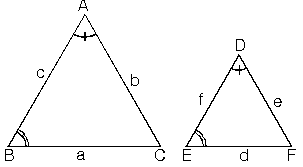
Karşılıklı ikişer açıları eş olan üçgenler benzerdir.
şekilde verilen üçgenlerde
İkişer açıları eş olduğundan, üçüncü açıları da eş olmak zorundadır. Dolayısıyla bu iki üçgen benzer üçgenlerdir.
m(C)=m(F)
Kenar – Açı – Kenar Benzerlik Teoremi
İki üçgenin karşılıklı ikişer kenarı orantılı ve bu kenarların oluşturduğu karşılıklı açılar eş ise, üçgenler benzerdir.
ABC üçgeni ile DEF üçgeninin BAC ve EDF açıları eş, bu açıların kenarları da orantılı ise, bu iki üçgen benzerdir.
BAC açısının kısa kenarının EDF açısının kısa kenarına oranı, BAC açısının uzun kenarının EDF açısının uzun kenarına oranına eşittir.
Kenar – Kenar – Kenar Benzerlik Teoremi
İki üçgenin karşılıklı bütün kenarları orantılı ise bu iki üçgen benzerdir.
şekilde verilen üçgenlerde
Kenarları orantılı olan ABC ve DEF benzer üçgenlerinde orantılı kenarları gören açılar eştir.
m(A) = m(D),
m(B) = m(E),
m(C) = m(F)
Temel Benzerlik Teoremi
ABC üçgeninde [DE] // [BC] ise yöndeş açılar eş olacağından ADE ~ ABC dir.
Buradan da
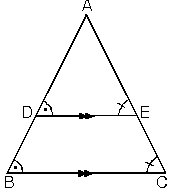
Ağırlık merkezinden çizilen paralel doğru kenarları 1 birime 2 birim oranında böler. ABC üçgeninde G ağırlık merkezi ve [KL] // [BC]
|AK|=2|KB|, |AL|=2|LC|
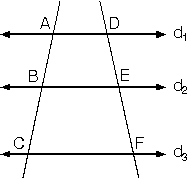
Tales Teoremi
Paralel doğrular kendilerini kesen doğruları aynı oranda bölerler. d1 // d2 // d3 doğruları için
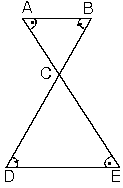
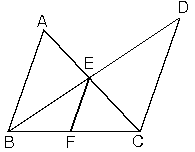
[AB] // [DE] ise oluşan içters açıların eşitliğinden, ABC ~ EDC olur. Buradan,
eşitliği elde edilir. Buna kelebek benzerliği de denir.
Benzerlik Özellikleri
Benzer üçgenlerin açıları karşılıklı olarak eş, diğer bütün elemanları orantılıdır.
ABC ~ DEF ise
Burada k ya benzerlik oranı denir.
Benzer üçgenlerde orantılı kenarlara ait yüksekliklerin oranı benzerlik oranına eşittir.
Benzer üçgenlerde orantılı kenarlara ait kenar-ortay uzunluklarının oranı benzerlik oranına eşittir.
Benzer üçgenlerde eş açılara ait açıortay uzunluklarının oranı benzerlik oranına eşittir.
Benzer üçgenlerin çevrelerinin oranı benzerlik oranına eşittir.
ABC üçgeninde içteğet çemberin yarıçapı ve çevrel çemberin yarıçapı , DEF üçgeninde içteğet çemberin yarıçapı ve çevrel çemberin yarıçapı olsun.
Alanlar oranı
Benzer üçgenlerin alanlarının oranı benzerlik oranının karesine eşittir.
Benzerlik oranı k = 1 olan üçgenler eş üçgenlerdir.
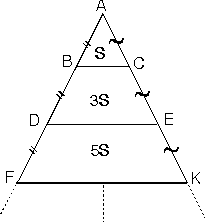
Kenarları eşit aralıklı paralellerle bölünmüş olan üçgenlerde alanlar 1, 3, 5, 7 … gibi tek sayılarla orantılı olarak artar.
[AB] // [EF] // [DC] benzerlik özelliklerinden,
|AB|.|FC|=|DC|.|BF|
Özel Teoremler
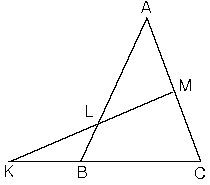
Menelaüs
ABC üçgeni KM doğru parçası ile şekildeki gibi kesiliyor ise
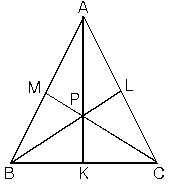
Seva
ABC üçgeni içerisinde alınan bir P noktası için,